/MAT/LAW48 (ZHAO)

Format

Definition

Comments

1. The stress-strain function is based on the formula published by Zhao:
   $$\sigma =\left(A+B{\epsilon }_p{}^n\right)+\left(C-D{\epsilon }_p{}^m\right)\cdot \ln \frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}+E_1{\dot{\epsilon }}^k$$
   Where,

   ${\epsilon }_p$

   Plastic strain

   $\dot{\epsilon }$

   Strain rate

2. Except for the strain rate formulation, the plasticity curve is strictly identical to a Johnson-Cook model:

   
   
   

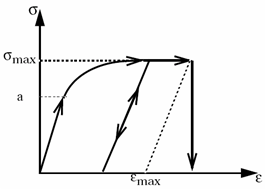
   However, compared to Johnson-Cook, the Zhao law allows a better approximation of a nonlinear strain rate dependent behavior.

3. Yield stress should be strictly positive.
4. The hardening exponent n must be less than 1.

   
   
   

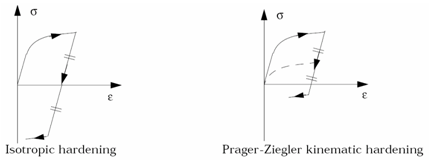
5. The iso-kinematic hardening parameter is defined as:
   • If C_hard = 0, hardening is a full isotropic model
   • If C_hard = 1, hardening uses the kinematic Prager-Ziegler model
   • If 0 < C_hard < 1, hardening is interpolated between the two models
6. If $\dot{\epsilon }\le {\dot{\epsilon }}_0$ , the term $\left(C-D{{\epsilon }_p}^m\right)\cdot \ln \frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}=0$ , and Equation 1 becomes:
   $$\sigma =\left(A+B{\epsilon }_p{}^n\right)+E_1{\dot{\epsilon }}^k$$
7. The strain rate filtering is used to smooth strain rate. It is only available for shell and solid elements.
8. When ${\epsilon }_p$ reaches ${\epsilon }_{\max }$ in one integration point, then based on the element type:
   • Shell elements: The corresponding shell element is deleted.
   • Solid elements: The deviatoric stress of the corresponding integral point is permanently set to 0, however, the solid element is not deleted.
9. If ${\epsilon }_1>{\epsilon }_{t1}$ ( ${\epsilon }_1$ is the largest principal strain), the stress is reduced as:
   $${\sigma }_{n+1}={\sigma }_n\left(\frac{{\epsilon }_{t2}-{\epsilon }_1}{{\epsilon }_{t2}-{\epsilon }_{t1}}\right)$$
10. If ${\epsilon }_1>{\epsilon }_{t2}$ , the stress is reduced to 0 (but the element is not deleted).