/MAT/LAW112 (PAPER or XIA)

Block Format Keyword The Paperboard law models an orthotropic and dissymmetric elasto-plastic material from proposed by Xia, 2002.

The basic principle is to fully uncouple the behavior in the plane of the paper sheet and the behavior out of the plane. A yield stress is defined for each directions of loading, in tension and compression.

Format


(1)	(3)	(5)	(7)	(8)	(9)
/MAT/LAW112/`mat_ID`/`unit_ID` or /MAT/PAPER/`mat_ID`/`unit_ID` or /MAT/XIA/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`₁	`E`₂	`E`₃	`Ires`	`Itab`	`I`_smooth
$ν_{21}$	`G`₁₂	`G`₂₃	`G`₁₃
`K`	`E3C`	`CC`
$ν_{1 p}$	$ν_{2 p}$	$ν_{4 p}$	$ν_{5 p}$

If Itab = 0, insert continuous yield stresses


(1)	(3)	(5)	(7)
`S01`	`A01`	`B01`	`C01`
`S02`	`A02`	`B02`	`C02`
`S03`	`A03`	`B03`	`C03`
`S04`	`A04`	`B04`	`C04`
`S05`	`A05`	`B05`	`C05`
`ASIG`	`BSIG`	`CSIG`
`TAU0`	`ATAU`	`BTAU`

If Itab = 1, insert tabulated yield stresses


(1)	(3)	(5)
`TAB_YLD1`	`MAT_Xscale1`	`MAT_Yscale1`
`TAB_YLD2`	`MAT_Xscale2`	`MAT_Yscale2`
`TAB_YLD3`	`MAT_Xscale3`	`MAT_Yscale3`
`TAB_YLD4`	`MAT_Xscale4`	`MAT_Yscale4`
`TAB_YLD5`	`MAT_Xscale5`	`MAT_Yscale5`
`TAB_YLDC`	`MAT_XscaleC`	`MAT_YscaleC`
`TAB_YLDS`	`MAT_XscaleS`	`MAT_YscaleS`

Definition


Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit Identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$
`E`_i	Young’s modulus in the i^th orthotropic direction. (Real)	$[Pa]$
$ν_{i j}$	Poisson's ratio related to the i^th and j^th orthotropic direction. (Real)
$G_{i j}$	Shear modulus related to the i^th and j^th orthotropic direction. (Real)	$[Pa]$
`Ires`	Resolution method for plasticity. = 0 Set to 2 = 1 NICE (Next Increment Correct Error) explicit method. = 2 (Default) Newton iterative method - cutting plane. (Integer)
`Itab`	Yield stresses computation. = 0 Continuous yield stresses. = 1 Tabulated yield stresses. (Integer)
`I`_smooth	Interpolation type (in case of tabulated yield function). = 1 (Default) Linear interpolation. = 2 Logarithmic interpolation base 10. =3 Logarithmic interpolation base n. (Integer)
`K`	In-plane yield surface exponent. Default = 1.0 (Real)
`E3C`	First elastic compression parameter. Default = `E`₃ (Real)	$[Pa]$
`CC`	Second elastic compression parameter. Default = 1.0 (Real)
$ν_{1 p}$	Tensile plastic Poisson’s ratio in direction 1. (Real)
$ν_{2 p}$	Tensile plastic Poisson’s ratio in direction 2. (Real)
$ν_{4 p}$	Compressive plastic Poisson’s ratio in direction 1. (Real)
$ν_{5 p}$	Compressive plastic Poisson’s ratio in direction 2. (Real)
`S0i`	Initial yield stress in the i^th direction of loading. Each direction is associated to a given loading direction following the order: i=1 Tension in orthotropic direction 1. i=2 Tension in orthotropic direction 2. i=3 In-plane shear. i=4 Compression in orthotropic direction 1. i=5 Compression in orthotropic direction 2. i=C Compression in out-of-plane direction 3. i=S Transverse shear direction. Default = 1.0e20 (Real)	$[Pa]$
`A0i`	First hardening parameter in the i^th direction of loading. (Real)	$[Pa]$
`B0i`	Second hardening parameter in the i^th direction of loading. (Real)
`C0i`	Third hardening parameter in the i^th direction of loading. (Real)	$[Pa]$
`ASIG`	Initial out-of-plane yield stress in compression. Default = 1.0e20 (Real)	$[Pa]$
`BSIG`	First out-of-plane hardening parameter in compression. (Real)	$[Pa]$
`CSIG`	Second out-of-plane hardening parameter in compression. (Real)
`TAU0`	Initial transverse shear yield stress. Default = 1.0e20 (Real)	$[Pa]$
`ATAU`	First transverse shear hardening parameter. (Real)	$[Pa]$
`BTAU`	Second transverse shear hardening parameter. (Real)
`TAB_YLDi`	Tabulated yield stress – plastic strain - strain rate function identifier in the i^th direction of loading. (Integer)
`MAT_Xscalei`	X scale factor of the tabulated yield – plastic strain - strain rate function in the i^th direction of loading. Default = 1.0 (Real)	$[Hz]$
`MAT_Yscalei`	Y scale factor of the tabulated yield – plastic strain - strain rate function in the i^th direction of loading. Default = 1.0 (Real)	$[Pa]$

▸Example (Paper)

#RADIOSS STARTER
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW112/1/1
Xia
#              RHO_I
            7.83E-10
#                 E1                  E2                  E3      Ires      Itab   Ismooth       
                4193                1554                1554         2         0         0
#               nu21                 G12                 G23                 G13  
              0.1011                 988                  76                  76
#                  K                 E3C                  CC                 
                 2.0                47.2               24.46                 
#               nu1p                nu2p                nu4p                nu5p
               0.555              0.1537                0.18               0.145
#                S01                 A01                 B01                 C01
                12.0                19.0               260.0               800.0
#                S02                 A02                 B02                 C02
                 6.5                40.0               160.0               250.0
#                S03                 A03                 B03                 C03       
                 6.0                11.0               100.0               125.0
#                S04                 A04                 B04                 C04
                 7.3                 6.0               160.0               300.0
#                S05                 A05                 B05                 C05
                 6.3                 9.0               310.0               225.0
#               ASIG                BSIG                CSIG
               16.55               16.55                3.16
#               TAU0                ATAU                BTAU
                 2.1                 9.0                 2.0    
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA

▸Example (Tabulated)

#RADIOSS STARTER
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|          
/MAT/LAW112/1/1
Xia_tab
#              RHO_I
            7.83E-10
#                 E1                  E2                  E3      Ires      Itab   Ismooth       
                4193                1554                1554         1         1         1
#               nu21                 G12                 G23                 G13 
              0.1011                 988                  76                  76
#                  K                 E3C                  CC                 
                 2.0                47.2               24.46                 
#               nu1p                nu2p                nu4p                nu5p
               0.555              0.1537                0.18               0.145
#           TAB_YLD1         MAT_Xscale1         MAT_Yscale1
                  25                 1.0                 1.0
#           TAB_YLD2         MAT_Xscale2         MAT_Yscale2
                  25                 1.0                0.35
#           TAB_YLD3         MAT_Xscale3         MAT_Yscale3
                  25                 1.0                0.75
#           TAB_YLD4         MAT_Xscale4         MAT_Yscale4
                  25                 1.0              0.6341
#           TAB_YLD5         MAT_Xscale5         MAT_Yscale5
                  25                 1.0                 0.5
#           TAB_YLDC         MAT_XscaleC         MAT_YscaleC
                  25                 1.0                 0.5
#           TAB_YLDS         MAT_XscaleS         MAT_YscaleS
                  25                 1.0                 0.5 
/FUNCT/46
ecoulement2   
#     plastic strain              stress                                                                                
                 0.0	           12.00
               0.012	 32.979020979021
               0.025	50.4615384615385
                0.05	            74.5
               0.075	90.9473684210526
                 0.1	102.909090909091
               0.125	          112.00
                0.15	119.142857142857
               0.175	124.903225806452
                 0.2	129.647058823529
                0.25	          137.00
                 0.3	142.434782608696
                 0.4	149.931034482759
                 0.5	154.857142857143
                 1.0	165.846153846154   
/TABLE/1/25
Yld Functions : plastic strain + strain rate dependency
#DIMENSION
         2
#   FCT_ID                   strain rate                                                     Scale_y
        46                           0.0                                                        1.00
        46                           1.0                                                        1.10
        46                           5.0                                                        1.15
        46                          10.0                                                        1.20
        46                         100.0                                                        1.25
        46                      100000.0                                                        1.35  
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata

Comments

To describe the behavior of the paperboard material law, the following orthotropic direction is considered.

Figure 1.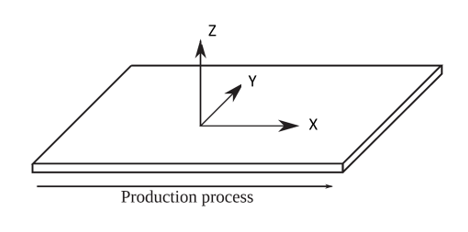
The elastic behavior of this material law is orthotropic.
The in-plane behavior should be fully uncoupled with the out-of-plane behavior, computed as:
${\begin{cases} σ_{x x} = C_{11} ε_{x x} + C_{12} ε_{y y} \\ σ_{y y} = C_{21} ε_{x x} + C_{22} ε_{y y} \\ σ_{x y} = G_{12} γ_{x y} \end{cases}$
With $C = \frac{1}{1 - ν_{12} ν_{21}} [\begin{matrix} E_{1} & ν_{12} E_{2} \\ ν_{21} E_{1} & E_{2} \end{matrix}]$
The transverse shear components are computed as:
${\begin{cases} σ_{y z} = G_{23} ε_{y z} \\ σ_{z x} = G_{21} ε_{z x} \end{cases}$
The out-of-plane elastic behavior (for solids only) is treated as a uniaxial equivalent problem. However, the computation of the stress may differ between tension and compression. The elasticity becomes nonlinear for compressive loadings.
$\begin{matrix} σ_{z z} = E_{3} ε_{z z}^{e} & if & ε_{z z}^{e} \geq 0 \\ σ_{z z} = E_{3 C} (1 - e^{- C_{c} ε_{z z}^{e}}) & if & ε_{z z}^{e} < 0 \end{matrix}$
In the Xia 2002 formulation, the in-plane yield criterion, denoted as $f$ , is defined as:
$f = {\sum_{I = 1}^{6} χ_{I} (\frac{σ : N_{I}}{σ_{Y}^{I}})}^{2 k} - 1$
Where,
$χ_{I} = {\begin{matrix} 1 & if & σ : N_{I} > 0 \\ 0 & otherwise \end{matrix}$

$χ_{I}$

Switching parameters.

$σ$

Cauchy stress tensor.

$N_{I}$

Normal direction of the yield planes.

$σ_{Y}^{I}$

Yield stresses.

$k$

Positive integer.

Each direction is associated to a given loading direction following the order defined below:

1

Tension in orthotropic direction 1.

2

Tension in orthotropic direction 2.

3

Positive in-plane shear.

4

Compression in orthotropic direction 1.

5

Compression in orthotropic direction 2.

6

Negative in-plane shear (same input as positive in-plane shear $σ_{Y}^{6} = σ_{Y}^{3}$ ).

The normal direction vector to the yield planes are:
$\begin{array}{l} N_{1} = [\begin{matrix} \frac{1}{\sqrt{1 + ν_{1 p}^{2}}} & - \frac{ν_{1 p}}{\sqrt{1 + ν_{1 p}^{2}}} & 0 & 0 & 0 & 0 \end{matrix}] \\ N_{2} = [\begin{matrix} - \frac{ν_{2 p}}{\sqrt{1 + ν_{2 p}^{2}}} & \frac{1}{\sqrt{1 + ν_{2 p}^{2}}} & 0 & 0 & 0 & 0 \end{matrix}] \\ N_{3} = [\begin{matrix} 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}] \\ N_{4} = [\begin{matrix} - \frac{1}{\sqrt{1 + ν_{4 p}^{2}}} & \frac{ν_{4 p}}{\sqrt{1 + ν_{4 p}^{2}}} & 0 & 0 & 0 & 0 \end{matrix}] \\ N_{5} = [\begin{matrix} \frac{ν_{5 p}}{\sqrt{1 + ν_{5 p}^{2}}} & - \frac{1}{\sqrt{1 + ν_{5 p}^{2}}} & 0 & 0 & 0 & 0 \end{matrix}] \\ N_{6} = [\begin{matrix} 0 & 0 & 0 & - 1 & 0 & 0 \end{matrix}] \end{array}$
Each direction $I$ is then associated to a specific yield stress whose expression is:
$\begin{matrix} σ_{Y}^{I} = S_{I}^{0} + A_{I}^{0} \tanh (B_{I}^{0} ε_{p}^{f}) + C_{I}^{0} ε_{p}^{f} & \begin{matrix} with & I \in [1, 6] \end{matrix} \end{matrix}$
Where, $ε_{p}^{f}$ is the in-plane equivalent plastic strain (associated to the yield function $f$ ).
The out-of-plane yield function is denoted as $g$ is defined as:
$g = - σ_{z z} - σ_{Y}^{C}$ with $σ_{Y}^{C} = A_{σ} + B_{σ} \exp (C_{σ} ε_{p}^{g})$
Where, $ε_{p}^{g}$ is the out-of-plane equivalent plastic strain (associated to the yield function $g$ ).
The transverse shear yield function is:
$h = \frac{\sqrt{σ_{y z}^{2} + σ_{z x}^{2}}}{σ_{Y}^{S}} - 1$
Where,

$σ_{Y}^{S} = τ_{0} + [A_{τ} - \min (0, σ_{z z}) B_{τ}] ε_{p}^{h}$

$ε_{p}^{h}$

Out-of-plane equivalent plastic strain (associated to the yield function $h$ ).

If the tabulated yield stress option is selected (Itab = 1), each yield stress is associated to a table (TAB_YLDi) to define the stress evolution with the plastic strain, at several plastic strain-rate. Two scale factors can be also defined in the X and Y direction for each table. In this case, the hardening parameters $S 0 i$ , $A 0 i$ , $B 0 i$ , $C 0 i$ , $A_{σ}$ , $B_{σ}$ , $C_{σ}$ , $τ_{0}$ , $A_{τ}$ , and $B_{τ}$ are ignored, and the yield stress becomes:
$\begin{array}{l} \begin{matrix} σ_{Y}^{I} = f_{Y}^{t a b_Y L D I} (ε_{p}^{f}, {\dot{ε}}_{p}^{f}) & I \in [1, 6] \end{matrix} \\ σ_{Y}^{C} = f_{Y}^{t a b_Y L D C} (ε_{p}^{g}, {\dot{ε}}_{p}^{g}) \\ σ_{Y}^{S} = f_{Y}^{t a b_Y L D S} (ε_{p}^{h}, {\dot{ε}}_{p}^{h}) \end{array}$
For output field, an equivalent “global” plastic strain is computed as:
$ε_{p} = \sqrt{{(ε_{p}^{f})}^{2} + {(ε_{p}^{g})}^{2} + {(ε_{p}^{h})}^{2}}$