/FAIL/ALTER

Format

Definition

Comments

1. This failure criteria is using the maximum stress as failure criterion. It is computed based on the strength of the material determined by initial cracks and the crack propagation velocity. Depending on mode switch flag, different failure propagation models between neighbor elements may be used.
2. When Irate=0, an exponential moving average filter is used, and the filtered stress is:
   $${\sigma }_f\left(t\right)=\alpha \sigma \left(t\right)+\left(1-\alpha \right)\sigma \left(t-\text{Δ}t\right)$$
   Where,

   ${\sigma }_f=\text{filtered stress}$

   $\alpha =\frac{2}{N_{cycles}+1}$

3. This failure model is compatible only with under-integrated shell elements (I_shell =24 and I_sh3n =2 are recommended) and not compatible with fully integrated shells. Also, although there is no restriction of the shell property that can be used, it is only compatible with one layer shell models.
4. The elements defined in the groups grsh4N and grsh3N should be along the edge of the windshield and will receive specific failure weakening.
5. This failure model is applied to shell elements that sandwich a polyvinyl butyral (PVB) solid element layer using coincident nodes. The entire assembly models a windshield.

   
   
   

   
   
   

6. The shell elements using this failure model should be oriented so that their normals point away the from the middle PVB.
7. The shell elements should have an offset applied to correctly model bending. This can be done using /PROP/TYPE51 I_pos=4.
8. The fracture limit depends on the location and the fracture state of surrounding elements. ¹
9. The fail_ID is used with /STATE/BRICK/FAIL and /INIBRI/FAIL and /PERTURB/FAIL/BIQUAD. There is no default value. If the line is blank, no value will be output for failure model variables in the /INIBRI/FAIL (written in .sta file with /STATE/BRICK/FAIL for brick and with /STATE/SHELL/FAIL for shell).
10. Ch. Brokmann extension ² defines additional fracture criteria for external glass surfaces only. It introduces initial stress on the glass surface, due to mechanical or chemical treatment. Statistical evaluation of micro flaws in the glass surface allows to define a probability of fracture using left-truncated Weibull stochastic distribution:

    with $i$ = 1,2 for bottom and top surface

    $$P(\sigma )=1-\exp \left[{{\displaystyle \left(\frac{{\tau }_i}{{\eta }_i}\right)}}^{{\beta }_i}-{{\displaystyle \left(\frac{\sigma }{{\eta }_i}\right)}}^{{\beta }_i}\right]$$

    Truncation point $\tau =0$ yields the well-known two-parameter Weibull distribution. The Brokmann model calculates the randomly oriented initial flaws in the glass and distributes them over all finite elements with different lengths and geometry. Crack growth may be expressed by the following differential equation:

    $$da=V_0.{{\displaystyle \left(\frac{Y\sigma \sqrt{\pi a}}{{{\displaystyle K}}_{IC}}\right)}}^{Exp\_n}dt$$

    Where, $Y$ is a flaw geometry factor obtained using Weibull distribution.

    Integral of Equation 3 will yield actual crack size, strongly dependent on stress rate. Actual stress intensity factors can be calculated and used in the fracture criteria.

    The interest of Brokmann’s model is that depending on the distribution parameters and failure stress value, it is possible to estimate the stochastic probability of failure.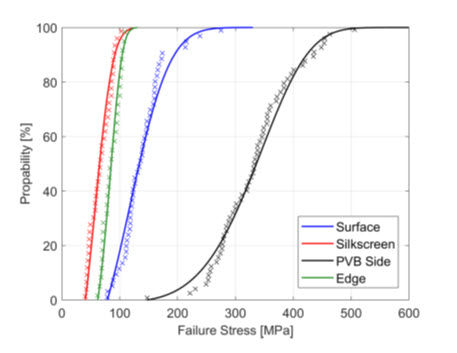

    
    
    

    After running a sufficient number of simulations with random initialization of glass flaws return a possibility to estimate a probability to reach a given value of the head injury criterion (HIC).

    
    
    

11. Flag Irate is automatically set to 0 when Ch. Brokmann criterion is used. It is then necessary to define the number of cycles for the stress filtering interval using exponential average.