Additional Details#
RotAxis#
Definition
The RotAxis class is a graphical representation of
the Instantaneous Axis of Rotation (IAOR). The IAOR is a line about which an object rotates
at any given moment in time.
This line changes direction and location as the object moves in space. It is critical for understanding spatial kinematics in engineering mechanics because at any moment in time the motion of a rigid body can be described as a pure rotation about the instantaneous axis.
To determine the IAOR, the following quantities are typically used:
the angular velocity vector of the rigid body \(\vec{\omega}\) expressed as the time derivative of its rotation matrix \(R\).
the translational velocity vector of any point on the rigid body.
The velocity \(\vec{\upsilon_{P}}\) for any point \(P\) at distance \(\vec{r}\) from the instantaneous axis of rotation can be expressed as the sum of the translational velocity \(\vec{\upsilon_{C}}\) of a reference point \(C\) and the tangential velocity \(\vec{\omega} \times \vec{r}\) due to the body rotation.
\(\vec{\upsilon_{P}} = \vec{\upsilon_{C}} + \vec{\omega} \times \vec{r}\)
where \(\vec{\upsilon_{C}}\) is the translational velocity of a reference point \(C\) and \(\vec{\omega} \times \vec{r}\) is the tangential velocity of the point P due to the rotation of the body.
Thus, knowing the position of a point \(\vec{r_{P}}\) and its translational velocity \(\vec{\upsilon_{P}}\), we can find the closest point \(\vec{r_{C}}\) on the instantaneous axis of rotation by projecting the position of point \(P\) onto the angular velocity vector \(\vec{\omega}\). The closest point \(\vec{r_{C}}\) on the IAOR can be found using the following equation:
This equation calculates the point \(\vec{r_{C}}\) on the IAOR by projecting the velocity of point \(P\), \(\vec{r_{P}}\) onto the direction of the IAOR, represented by the angular velocity vector \(\vec{\omega}\).
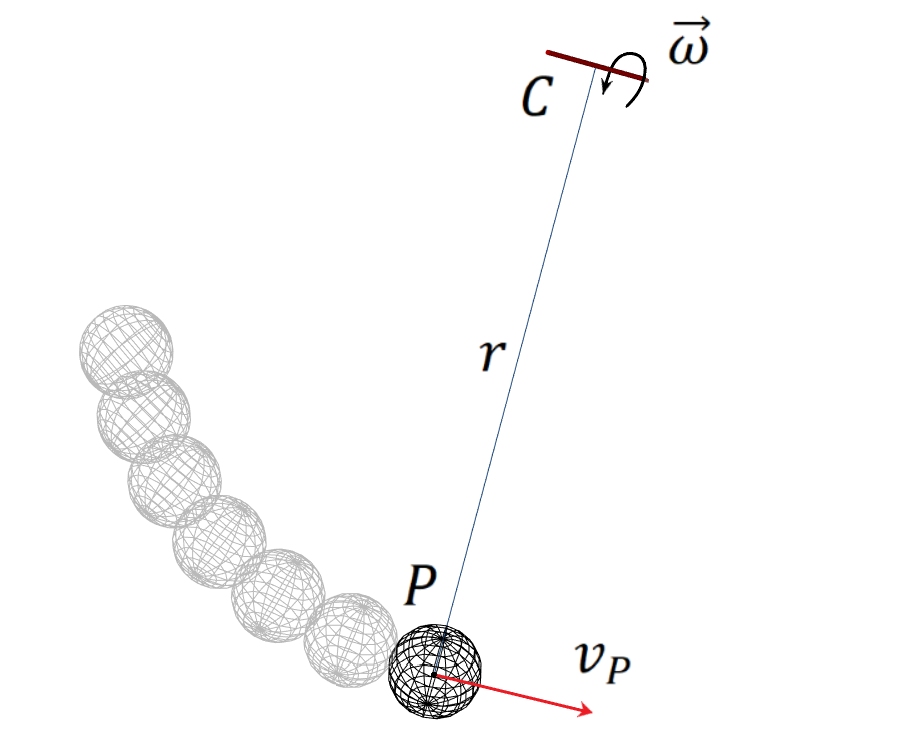
Figure 1. The instantaneous axis of rotation for the pendulum example.#
At any instant in time, a rolling body may be considered to be in pure rotation about the IAOR, which passes through the point of contact. The axis is translating forward with speed equal to the linear velocity of the rolling body’s center of mass.
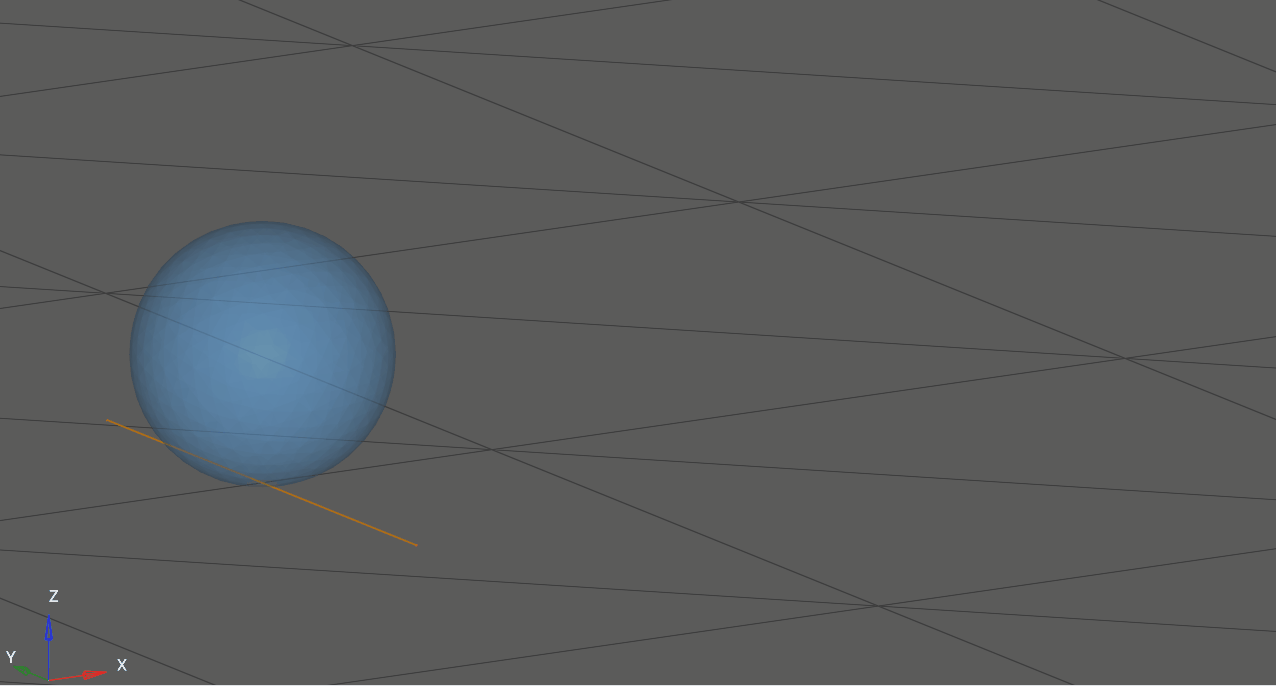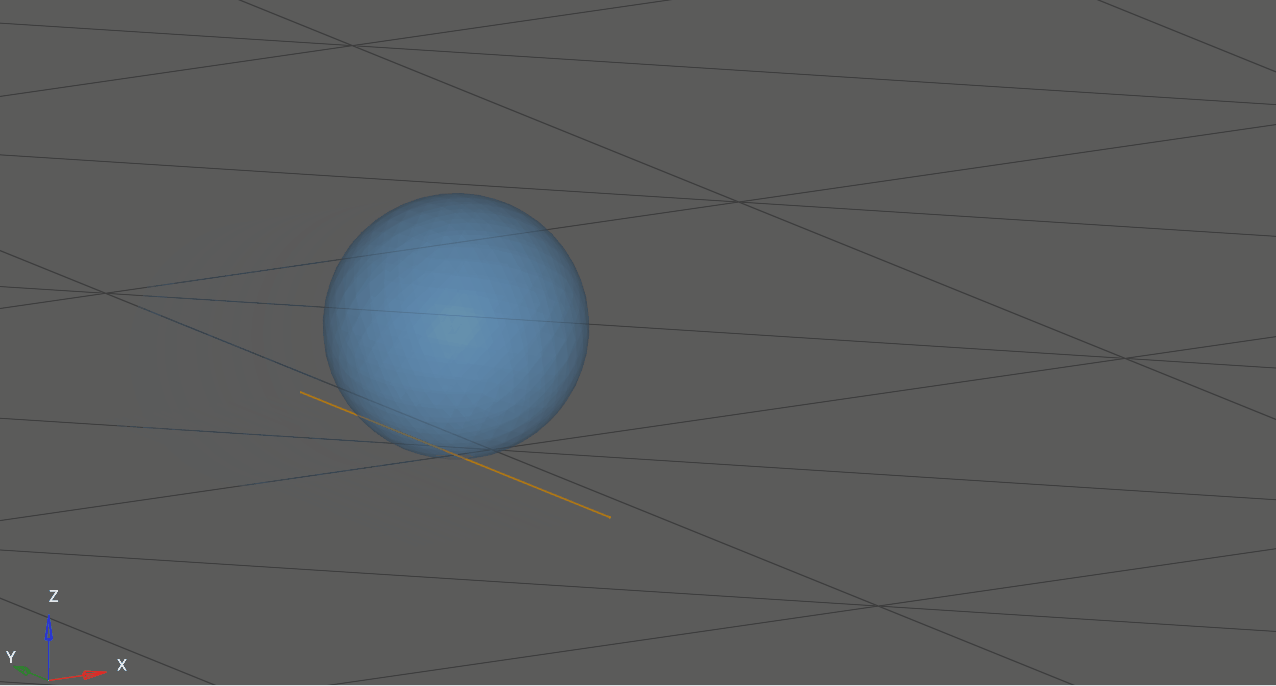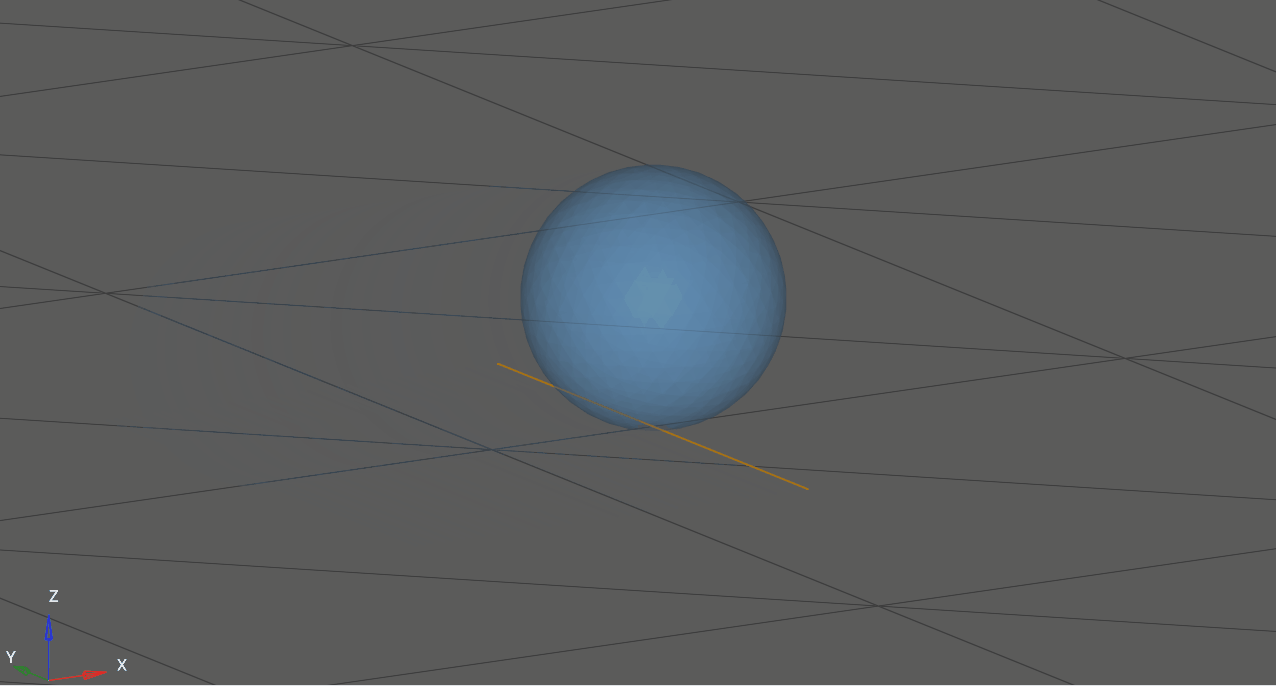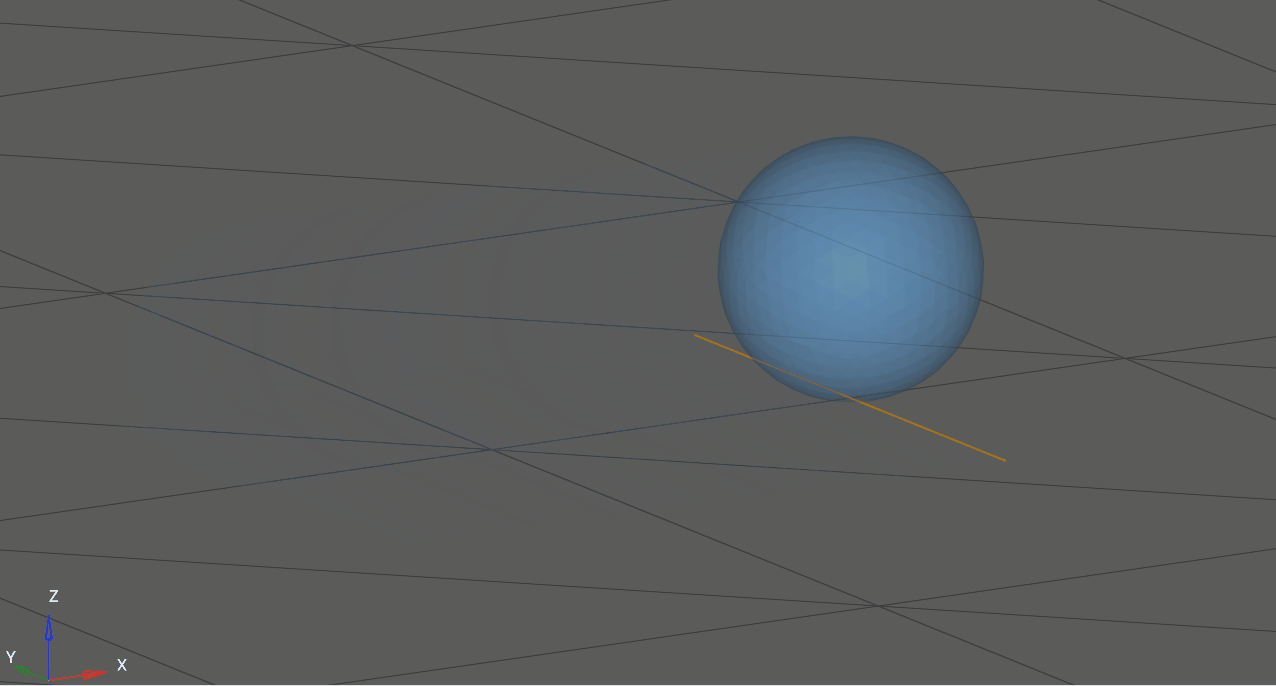
Figure 2. The instantaneous axis of rotation for a purely-rolling sphere on a flat surface.#
Visualization
Using the above equations, the coordinates of a point on the instantaneous axis can be found, for which the distance between the body’s center of mass and said point is shortest. Similarly, we can determine the point for which the distance between the axis and the global origin is shortest. The line that connects these two points is the instantaneous axis of rotation.
In msolve, the axis is displayed as a meshed cylinder with its base featuring \(n\) number of nodes. For a purely rotating body, the axis will pass through its center of mass. For example, the instantaneous axis for a sphere of radius \(r = 5 mm\), located at \(z = 20 mm\), purely rotating about the global \(Z\) axis, having a base with \(n = 8\), is displayed as shown in Fig. 2 below.
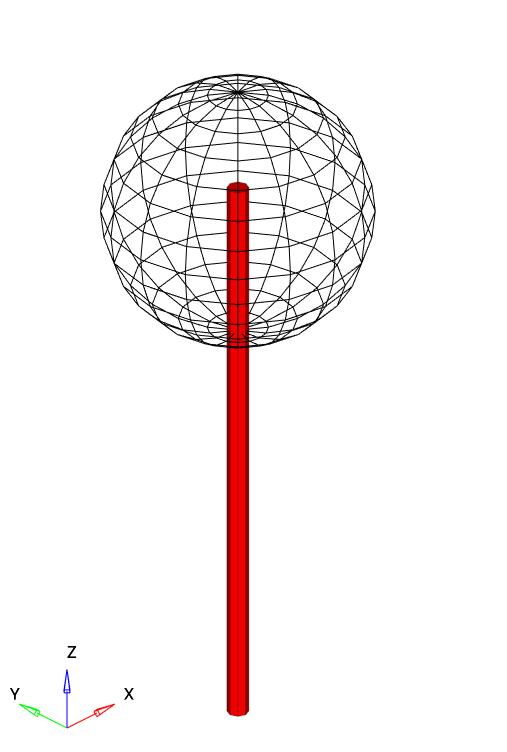
Figure 3. The instantaneous axis of rotation for a purely-rotating sphere about the global Z axis.#
Note
You can change the length and width of the cylinder representing the axis by using the scale and radius attributes respectively.