
For certain applications, a transfer function representation of the linearized system may be more desirable than a state-space representation. Analyze > Transfer Function Info presents a linearized system in transfer function form and includes the following information:
•The numerator and denominator polynomials are presented in powers of the complex variable s defined as:

where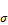

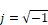
•The gain of the transfer function
•The factors of the numerator (zeros) and the denominator (poles). The zeros and poles may appear in the following format:
(real-part, imaginary-part)
The transfer function is computed from the state-space matrices using a similarity transformation. The poles and zeros are computed by converting the numerator and denominator polynomials to square matrices and computing the corresponding eigenvalues.
|
|
|
If numerical round-off errors occur during the factoring process, they can be corrected by using Analyze > Preferences.
To generate a linear transfer function
1. Prepare the system for linearization.
2. Choose Analyze > Transfer Function Info.
3. Resize or zoom in on the plot for better viewing.