Zeros and poles are computed by converting the linearized numerator and denominator polynomials to square matrices and then computing the corresponding eigenvalues. In general, this method is reliable and robust; however, to compensate for numerical round-off error (a floating-point number only holds 15 digits of precision), you may want to clean the numerator and denominator polynomials prior to computing the poles and zeros. This is because very small terms in the transfer function (for example, 1e-15) become very large terms after a matrix inverse (part of the operation of finding eigenvalues), resulting in erroneously large poles. To fix the problem, set a threshold value under which Embed will treat a coefficient as 0. You can set thresholds for the numerator or denominator polynomial, or the eigenvalues themselves.
To correct the polynomials
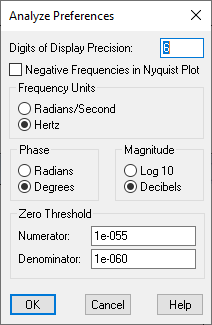
1. Choose Analyze > Preferences.

2. In Digits Of Display Precision, enter a number that indicates the round-off for poles and zeros.
3. Under Zero Threshold, enter the appropriate numerator and denominator values. Based on your knowledge of the system, you may raise or lower the threshold for 0 treatment. The defaults are 1e-011 (numerator) and 1e-060 (denominator). Polynomial coefficients whose absolute values are less than these values multiplied by the absolute value of the largest coefficient in the polynomial will be set to 0.
For example, consider the following:
s^0 20000
s^1 1000
s^2 1e-10
The s^2 coefficient contains a numerical error. The actual value should be exactly 0. To achieve this, the Numerator parameter should be set to a value less than (1e-10)*(20000) or 2e-6 to remove the error and set the s^2 coefficient to 0.
4. Click OK, or press ENTER.