/MAT/LAW14 (COMPSO)

Format

Definition

Comments

1. This material requires an orthotropic solid property (/PROP/TYPE6 (SOL_ORTH), /PROP/TYPE21 (TSH_ORTH) or /PROP/TYPE22 (TSH_COMP)). It can only be used with solid elements for a 3-dimensional analysis. This law is compatible with 10-node tetrahedron and 4-node tetrahedron elements. The orthotropic material directions are specified in the property entries.
2. Stress-strain relation in elastic phase.

   The stresses and strains are connected as:

   $${\epsilon }_{11}=\frac{1}{E_{11}}{\sigma }_{11}-\frac{{\nu }_{21}}{E_{22}}{\sigma }_{22}-\frac{{\nu }_{31}}{E_{33}}{\sigma }_{33}$$
   $${\epsilon }_{22}=\frac{1}{E_{22}}{\sigma }_{22}-\frac{{\nu }_{21}}{E_{11}}{\sigma }_{11}-\frac{{\nu }_{32}}{E_{33}}{\sigma }_{33}$$
   $${\epsilon }_{33}=\frac{1}{E_{33}}{\sigma }_{33}-\frac{{\nu }_{13}}{E_{11}}{\sigma }_{11}-\frac{{\nu }_{23}}{E_{22}}{\sigma }_{22}$$

   ${\gamma }_{12}=\frac{1}{2G_{12}}{\sigma }_{12}$ $\frac{{\nu }_{21}}{E_{22}}=\frac{{\nu }_{12}}{E_{11}}$

   ${\gamma }_{23}=\frac{1}{2G_{23}}{\sigma }_{23}$ $\frac{{\nu }_{32}}{E_{33}}=\frac{{\nu }_{23}}{E_{22}}$

   ${\gamma }_{31}=\frac{1}{2G_{31}}{\sigma }_{31}$ $\frac{{\nu }_{13}}{E_{11}}=\frac{{\nu }_{31}}{E_{33}}$

   Where,

   ${\epsilon }_{{}_{ij}}$

   Strains

   ${\sigma }_{{}_{ij}}$

   Stresses

   ${\gamma }_{{}_{12}}$ , ${\gamma }_{{}_{23}}$ and ${\gamma }_{{}_{31}}$

   Distortions in the corresponding material directions

   For example, for ${\gamma }_{{}_{12}}$ :

   
   
   

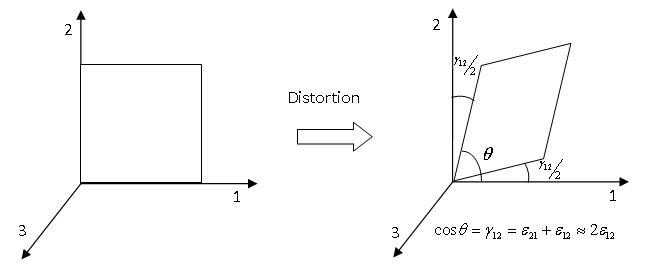
3. Tsai-Wu criterion
   The material is assumed to be elastic until the Tsai-Wu criterion is fulfilled. After exceed the Tsai-Wu criterion limit $\mathrm{F}(W_p^{*},\dot{\epsilon })$ , the material becomes nonlinear.

   • If $\mathrm{F}(\sigma )<\mathrm{F}(W_p^{*},\dot{\epsilon })$ : elastic
   • If $\mathrm{F}(\sigma )>\mathrm{F}(W_p^{*},\dot{\epsilon })$ : nonlinear
   Where,

   • Stress $\mathrm{F}\left(\sigma \right)$ in element for Tsai-Wu criterion computed as:
     $$\begin{array}{l}\mathrm{F}\left(\sigma \right)=F_1{\sigma }_1+F_2{\sigma }_2+F_3{\sigma }_3\\ \begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}+F_{11}{\sigma }_1^2+F_{22}{\sigma }_2^2+F_{33}{\sigma }_3^2+F_{44}{\sigma }_{12}^2+F_{55}{\sigma }_{23}^2+F_{66}{\sigma }_{31}^2\\ \begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}\begin{array}{c}\end{array}+2F_{12}{\sigma }_1{\sigma }_2+2F_{23}{\sigma }_2{\sigma }_3+2F_{13}{\sigma }_1{\sigma }_3\end{array}$$
   The coefficients of the Tsai-Wu criterion are determined from the limiting stresses when the material becomes nonlinear in directions 1, 2, 3 or 12, 23, 31 (shear) in compression or tension as:

   $F_1=-\frac{1}{{\sigma }_{1y}^c}+\frac{1}{{\sigma }_{1y}^t}$	$F_2=-\frac{1}{{\sigma }_{2y}^c}+\frac{1}{{\sigma }_{2y}^t}$	$F_3=-\frac{1}{{\sigma }_{3y}^c}+\frac{1}{{\sigma }_{3y}^t}$
   $F_{11}=\frac{1}{{\sigma }_{1y}^c{\sigma }_{1y}^t}$	$F_{22}=\frac{1}{{\sigma }_{2y}^c{\sigma }_{2y}^t}$	$F_{33}=\frac{1}{{\sigma }_{3y}^c{\sigma }_{3y}^t}$
   $F_{44}=\frac{1}{{\sigma }_{12y}^c{\sigma }_{12y}^t}$	$F_{55}=\frac{1}{{\sigma }_{23y}^c{\sigma }_{23y}^t}$	$F_{66}=\frac{1}{{\sigma }_{31y}^c{\sigma }_{31y}^t}$
   $F_{12}=-\frac{1}{2}\sqrt{\left(F_{11}{F}_{22}\right)}$	$F_{23}=-\frac{1}{2}\sqrt{\left(F_{22}{F}_{33}\right)}$	$F_{13}=-\frac{1}{2}\sqrt{\left(F_{11}{F}_{33}\right)}$

   The nonlinear behavior in directions 2 and 3 is assumed to be the same to represent the composite matrix material. It is assumed that yield stresses of the composite matrix material (in directions 2 and 3) are related as:

   ${\sigma }_{3y}^c={\sigma }_{2y}^c$	${\sigma }_{3y}^t={\sigma }_{2y}^t$
   ${\sigma }_{31y}^c={\sigma }_{12y}^c$	${\sigma }_{31y}^t={\sigma }_{12y}^t$

   • $\mathrm{F}\left(W_p^{*},\dot{\epsilon }\right)$ is the variable Tsai-Wu criterion limit defined:
     $$\mathrm{F}\left(W_p^{*},\dot{\epsilon }\right)=\left[1+B{\left(W_p^{*}\right)}^n\right]\cdot \left[1+c\cdot \ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\right]$$
     Where,

     $W_p{}^{ref}$

     Reference plastic work

     $W_p^{*}=\frac{W_p}{W_p^{ref}}$

     Relative plastic work

     $B$

     Plastic hardening parameter

     $n$

     Plastic hardening exponent

     ${\dot{\epsilon }}_0$

     Reference true strain rate

     $c$

     Strain rate coefficient

     $\mathrm{F}\left(W_p^{*},\dot{\epsilon }\right)$ the maximum value of the Tsai-Wu criterion limit depends on ICC:

     If ICC=1

     $f_{\max }\cdot \left(1+c\cdot \ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_o}\right)\right)$

     If ICC=2

     $f_{\max }$

     Where, $f_{\max }={\left(\frac{{\sigma }_{\max }}{{\sigma }_y}\right)}^2$

4. Stress damage

   When the limiting stress value of ${\sigma }_{ti}$ is reached in tension, then the corresponding stress value is scaled as ${\sigma }_i^{reduced}=(1-D_i){\sigma }_{ti}$ . The value of $D_i$ is updated on each time step $D_i={\displaystyle \sum _i{\delta }_i}$ . After $D_i$ reaches the value of 1 the stress in corresponding direction is set to 0. The damage is irreversible, if a value of $D_i$ is attained the material will not reach any lower damage value.

5. Fiber reinforcement

   These parameters allow the user to define additional fiber reinforcement in the 11 direction. Additional stress in direction 11 will be added equal to $\alpha \cdot E_f\cdot {\epsilon }_{11}$ .