LossyGear
Gear with mesh efficiency and bearing friction (stuck/rolling possible)
![]()
Library
Modelica/Mechanics/Rotational/Components
Description
This component models the gear ratio and the losses ofa standard gear box in a reliable way including the stuck phasesthat may occur at zero speed. The gear boxes that canbe handled are fixed in the ground or on a moving support, have one input and oneoutput shaft, and are essentially described by the equations:
flange_a.phi = i*flange_b.phi;-(flange_b.tau - tau_bf_b) = i*eta_mf*(flange_a.tau - tau_bf_a);// or -flange_b.tau = i*eta_mf*(flange_a.tau - tau_bf_a - tau_bf_b/(i*eta_mf));
where
- i is the constant gear ratio,
- eta_mf = eta_mf(w_a) is the mesh efficiency due to the friction between the teeth of the gear wheels,
- tau_bf_a = tau_bf_a(w_a) is the bearing friction torque on the flange_a side,
- tau_bf_b = tau_bf_b(w_a) is the bearing friction torque on the flange_b side, and
- w_a = der(flange_a.phi) is the speed of flange_a
The loss terms "eta_mf", "tau_bf_a" and "tau_bf_b" are functions of theabsolute value of the input shaft speed w_a and of the energyflow direction. They are defined by parameter lossTable[:,5] where the columns of this table have the followingmeaning:
| |w_a| | eta_mf1 | eta_mf2 | |tau_bf1| | |tau_bf2| |
| … | … | … | … | … |
| … | … | … | … | … |
with
| |w_a| | Absolute value of angular velocity of input shaft flange_a |
| eta_mf1 | Mesh efficiency in case that flange_a is driving |
| eta_mf2 | Mesh efficiency in case that flange_b is driving |
| |tau_bf1| | Absolute resultant bearing friction torque with respect to flange_a in case that flange_a is driving (= |tau_bf_a*eta_mf1 + tau_bf_b/i|) |
| |tau_bf2| | Absolute resultant bearing friction torque with respect to flange_a in case that flange_b is driving (= |tau_bf_a/eta_mf2 + tau_bf_b/i|) |
With these variables, the mesh efficiency and the bearing frictionare formally defined as:
if (flange_a.tau - tau_bf_a)*w_a > 0 or (flange_a.tau - tau_bf_a) == 0 and w_a > 0 then eta_mf := eta_mf1 tau_bf := tau_bf1elseif (flange_a.tau - tau_bf_a)*w_a < 0 or (flange_a.tau - tau_bf_a) == 0 and w_a < 0 then eta_mf := 1/eta_mf2 tau_bf := tau_bf2else // w_a == 0 eta_mf and tau_bf are computed such that der(w_a) = 0end if;-flange_b.tau = i*(eta_mf*flange_a.tau - tau_bf);
Note, that the losses are modeled in a physically meaningful way takinginto account that at zero speed the movement may be locked dueto the friction in the gear teeth and/or in the bearings.Due to this important property, this component can be used insituations where the combination of the componentsModelica.Mechanics.Rotational.IdealGear andModelica.Mechanics.Rotational.GearEfficiency will fail because,e.g., chattering occurs when using theModelica.Mechanics.Rotational.GearEfficiency model.
Acknowledgement
- The essential idea to model efficiency in this way is from Christoph Pelchen, ZF Friedrichshafen.
- The article (Pelchen et.al. 2002), see Literature below, and the first implementation of LossyGear (up to version 3.1 of package Modelica) contained a bug leading to a non-converging solution in cases where the driving side is not obvious. This was pointed out by Christian Bertsch and Max Westenkirchner, Bosch, and Christian Bertsch proposed a concrete solution how to fix this bug, see Literature below.
Literature
- Pelchen C.,Schweiger C.,and Otter M.:"Modelingand Simulating the Efficiency of Gearboxes and of Planetary Gearboxes," inProceedings of the 2nd International Modelica Conference, Oberpfaffenhofen, Germany,pp. 257-266, The Modelica Association and Institute of Robotics and Mechatronics,Deutsches Zentrum für Luft- und Raumfahrt e. V., March 18-19, 2002.
- Bertsch C. (2009):"Problemwith model LossyGear and a proposed solution",Ticket #108,Sept. 11, 2009.
Parameters
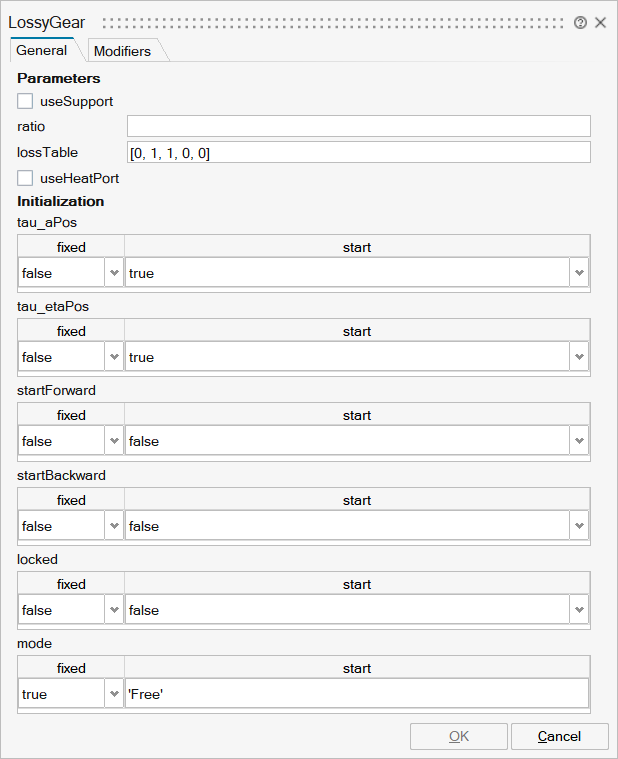
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo_useSupport | useSupport | = true, if support flange enabled, otherwise implicitly grounded | Number | 0 |
mo_ratio | ratio | Transmission ratio (flange_a.phi/flange_b.phi) | Scalar | |
mo_lossTable | lossTable | Array for mesh efficiencies and bearing friction depending on speed | Matrix of size Mx5 | |
mo_useHeatPort | useHeatPort | = true, if heatPort is enabled | Number | 0 |
mo_eta_mf1_0 | eta_mf1_0 | Scalar | ||
mo_eta_mf2_0 | eta_mf2_0 | Scalar | ||
mo_tau_bf1_0 | tau_bf1_0 | Scalar | ||
mo_tau_bf2_0 | tau_bf2_0 | Scalar | ||
mo_tau_bf_a_0 | tau_bf_a_0 | Scalar | ||
mo_tau_aPos | tau_aPos | tau_aPos | Structure | |
mo_tau_aPos/fixed | fixed | Cell of scalars | true | |
mo_tau_aPos/start | start | Cell of scalars | true | |
mo_tau_etaPos | tau_etaPos | tau_etaPos | Structure | |
mo_tau_etaPos/fixed | fixed | Cell of scalars | true | |
mo_tau_etaPos/start | start | Cell of scalars | true | |
mo_startForward | startForward | startForward | Structure | |
mo_startForward/fixed | fixed | Cell of scalars | true | |
mo_startForward/start | start | Cell of scalars | true | |
mo_startBackward | startBackward | startBackward | Structure | |
mo_startBackward/fixed | fixed | Cell of scalars | true | |
mo_startBackward/start | start | Cell of scalars | true | |
mo_locked | locked | locked | Structure | |
mo_locked/fixed | fixed | Cell of scalars | true | |
mo_locked/start | start | Cell of scalars | true | |
mo_mode | mode | mode | Structure | |
mo_mode/fixed | fixed | Cell of scalars | true | |
mo_mode/start | start | Cell of scalars |
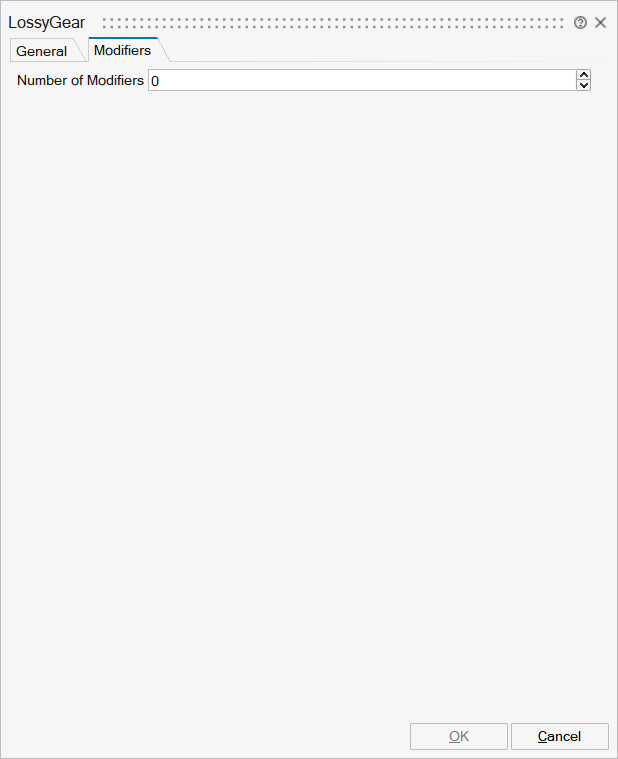
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo__nmodifiers | Number of Modifiers | Specifies the number of modifiers | Number | |
mo__modifiers | Modifiers | Add new modifier | Structure | |
mo__modifiers/varname | Variable name | Cell of strings | 'phi_support' | |
mo__modifiers/attribute | Attribute | Cell of strings | 'start' | |
mo__modifiers/value | Value |
Ports
| Name | Type | Description | IO Type | Number |
|---|---|---|---|---|
flange_a | implicit | Flange of left shaft | input | 1 |
flange_b | implicit | Flange of right shaft | output | 1 |
Port 3 | implicit | Support/housing of component | input | mo_useSupport |
Port 4 | implicit | Optional port to which dissipated losses are transported in form of heat | input | mo_useHeatPort |