Filter
Continuous low pass, high pass, band pass or band stop IIR-filter of type CriticalDamping, Bessel, Butterworth or ChebyshevI
![]()
Library
Modelica/Blocks/Continuous
Description
This blocks models various types of filters:
low pass, high pass, band pass, and band stop filters
using various filter characteristics:
CriticalDamping, Bessel, Butterworth, Chebyshev Type I filters
By default, a filter block is initialized in steady-state, in order toavoid unwanted oscillations at the beginning. In special cases, it might beuseful to select one of the other initialization options under tab"Advanced".
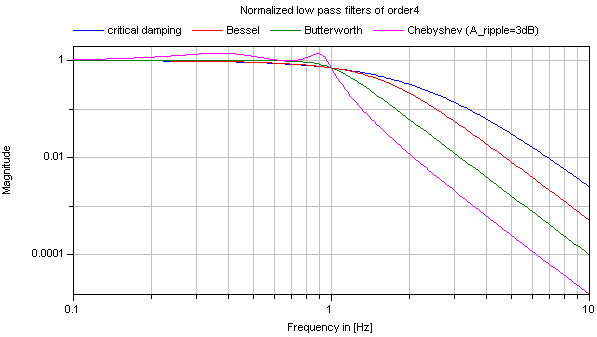
Typical frequency responses for the 4 supported low pass filter typesare shown in the next figure:
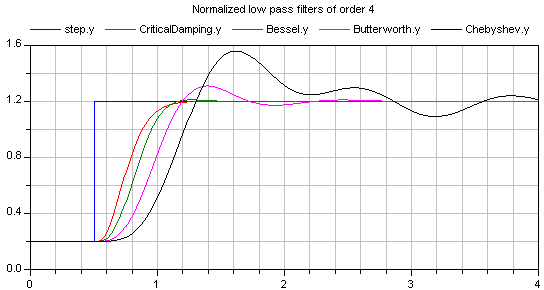
The step responses of the same low pass filters are shown in the next figure,starting from a steady state initial filter with initial input = 0.2:
Obviously, the frequency responses give a somewhat wrong impressionof the filter characteristics: Although Butterworth and Chebyshevfilters have a significantly steeper magnitude as theCriticalDamping and Bessel filters, the step responses ofthe latter ones are much better. This means for example, thata CriticalDamping or a Bessel filter should be selected,if a filter is mainly used to make a non-linear inverse modelrealizable.
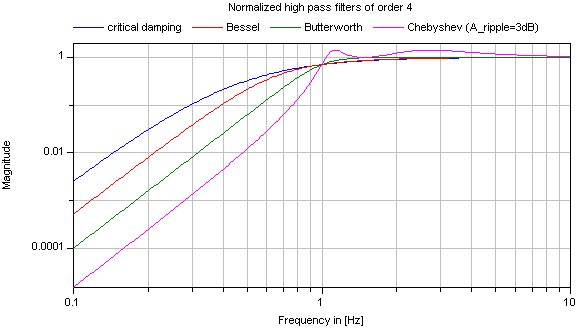
Typical frequency responses for the 4 supported high pass filter typesare shown in the next figure:
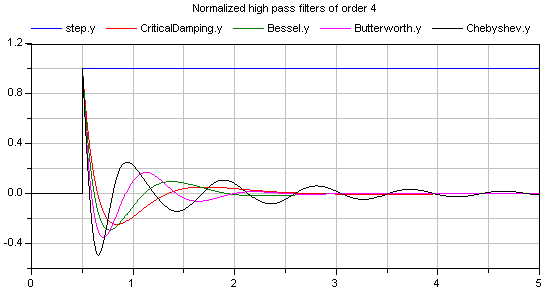
The corresponding step responses of these high pass filters areshown in the next figure:
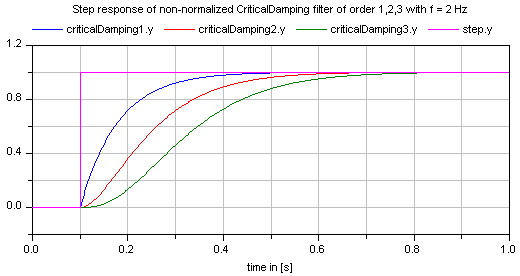
All filters are available in normalized (default) and non-normalized form.In the normalized form, the amplitude of the filter transfer functionat the cut-off frequency f_cut is -3 dB (= 10^(-3/20) = 0.70794..).Note, when comparing the filters of this function with other software systems,the setting of "normalized" has to be selected appropriately. For example, the signal processingtoolbox of MATLAB provides the filters in non-normalized form andtherefore a comparison makes only sense, if normalized = falseis set. A normalized filter is usually better suited for applications,since filters of different orders are "comparable",whereas non-normalized filters usually require to adapt thecut-off frequency, when the order of the filter is changed.See a comparison of "normalized" and "non-normalized" filters at hand ofCriticalDamping filters of order 1,2,3:
Implementation
The filters are implemented in the following, reliable way:
- A prototype low pass filter with a cut-off angular frequency of 1 rad/s is constructed from the desired analogFilter and the desired normalization.
- This prototype low pass filter is transformed to the desired filterType and the desired cut-off frequency f_cut using a transformation on the Laplace variable "s".
- The resulting first and second order transfer functions are implemented in state space form, using the "eigen value" representation of a transfer function:
// second order block with eigen values: a +/- jb der(x1) = a*x1 - b*x2 + (a^2 + b^2)/b*u; der(x2) = b*x1 + a*x2; y = x2;
The dc-gain from the input to the output of this block is one and the selected states are in the order of the input (if "u" is in the order of "one", then the states are also in the order of "one"). In the "Advanced" tab, a "nominal" value for the input "u" can be given. If appropriately selected, the states are in the order of "one" and then step-size control is always appropriate.
References
- Tietze U., and Schenk C. (2002):
- Halbleiter-Schaltungstechnik. Springer Verlag, 12. Auflage, pp. 815-852.
Parameters
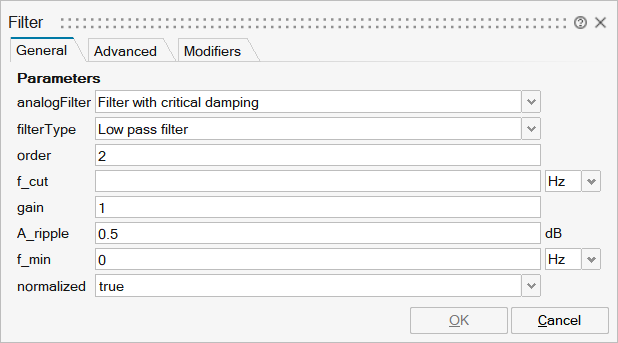
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo_analogFilter | analogFilter | Analog filter characteristics (CriticalDamping/Bessel/Butterworth/ChebyshevI) | Structure | |
mo_analogFilter/choice1 | Filter with critical damping | Number | 0 | |
mo_analogFilter/choice2 | Bessel filter | Number | 0 | |
mo_analogFilter/choice3 | Butterworth filter | Number | 0 | |
mo_analogFilter/choice4 | Chebyshev I filter | Number | 0 | |
mo_filterType | filterType | Type of filter (LowPass/HighPass/BandPass/BandStop) | Structure | |
mo_filterType/choice1 | Low pass filter | Number | 0 | |
mo_filterType/choice2 | High pass filter | Number | 0 | |
mo_filterType/choice3 | Band pass filter | Number | 0 | |
mo_filterType/choice4 | Band stop / notch filter | Number | 0 | |
mo_order | order | Order of filter | Scalar | |
mo_f_cut | f_cut | Cut-off frequency | Scalar | |
mo_gain | gain | Gain (= amplitude of frequency response at zero frequency) | Scalar | |
mo_A_ripple | A_ripple | Pass band ripple for Chebyshev filter (otherwise not used); > 0 required | Scalar | |
mo_f_min | f_min | Band of band pass/stop filter is f_min (A=-3db*gain) .. f_cut (A=-3db*gain) | Scalar | |
mo_normalized | normalized | = true, if amplitude at f_cut = -3db, otherwise unmodified filter | Scalar | true |
mo_nx | nx | Scalar | ||
mo_ncr | ncr | Scalar | ||
mo_nc0 | nc0 | Scalar | ||
mo_na | na | Scalar | ||
mo_nr | nr | Scalar | ||
mo_cr | cr | Vector | ||
mo_c0 | c0 | Vector | ||
mo_c1 | c1 | Vector | ||
mo_r | r | Vector | ||
mo_a | a | Vector | ||
mo_b | b | Vector | ||
mo_ku | ku | Vector | ||
mo_k1 | k1 | Vector | ||
mo_k2 | k2 | Vector |
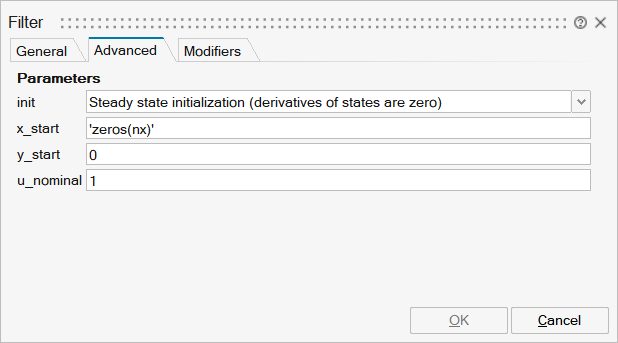
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo_init | init | Type of initialization (no init/steady state/initial state/initial output) | Structure | |
mo_init/choice1 | No initialization (start values are used as guess values with fixed=false) | Number | 0 | |
mo_init/choice2 | Steady state initialization (derivatives of states are zero) | Number | 0 | |
mo_init/choice3 | Initialization with initial states | Number | 0 | |
mo_init/choice4 | Initialization with initial outputs (and steady state of the states if possible) | Number | 0 | |
mo_x_start | x_start | Initial or guess values of states | Vector | |
mo_y_start | y_start | Initial value of output | Scalar | |
mo_u_nominal | u_nominal | Nominal value of input (used for scaling the states) | Scalar |
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo__nmodifiers | Number of Modifiers | Specifies the number of modifiers | Number | |
mo__modifiers | Modifiers | Add new modifier | Structure | |
mo__modifiers/varname | Variable name | Cell of strings | 'uu' | |
mo__modifiers/attribute | Attribute | Cell of strings | 'start' | |
mo__modifiers/value | Value |
Ports
| Name | Type | Description | IO Type | Number |
|---|---|---|---|---|
u | implicit | Connector of Real input signal | input | 1 |
y | implicit | Connector of Real output signal | output | 1 |