 Package Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend
Package Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.BendIcon for general information packages
 Package Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend
Package Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend
This icon indicates classes containing only documentation, intended for general description of, e.g., concepts and features of a package.
Extends from Modelica.Icons.Information (Icon for general information packages).
| Name | Description |
|---|---|
dp_curvedOverall | |
dp_edgedOverall |
 Class Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend.dp_curvedOverall
Class Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend.dp_curvedOverall
Calculation of pressure loss in curved bends at overall flow regime for incompressible and single-phase fluid flow through circular cross sectional area considering surface roughness.
This function shall be used inside of the restricted limits according to the referenced literature.
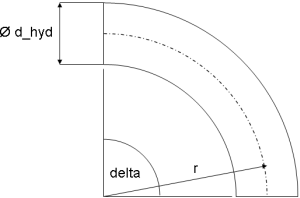
The pressure loss dp for curved bends is determined by:
dp = zeta_TOT * (rho/2) * velocity^2
with
rho |
as density of fluid [kg/m3], |
velocity |
as mean velocity [m/s], |
zeta_TOT |
as pressure loss coefficient [-]. |
Curved bends with relative curvature radius R_0/d_hyd ≤ 3 according to [Idelchik 2006, p. 357, diag. 6-1]
The pressure loss of curved bends is similar to its calculation in straight pipes. There are three different flow regimes observed (laminar,transition,turbulent). The turbulent regime is further separated into sections with a dependence or independence of the local resistance coefficient (zeta_LOC ) on Reynolds number. The local resistance coefficient (zeta_LOC) of a curved bend is calculated in dependence of the flow regime as follows:
Laminar regime (Re ≤ Re_lam_leave):
zeta_LOC = A2/Re + A1*B1*C1
Transition regime (Re_lam_leave ≤ 4e4)
This calculation is done using a smoothing function interpolating between the laminar and the first turbulent flow regime.
Turbulent regime (4e4 ≤ 3e5) with dependence of local resistance coefficient on Reynolds number:
zeta_LOC = k_Re * (A1*B1*C1)
where k_Re depends on the relative curvature radius R_0/d_hyd
k_Re = 1 + 4400/Re for 0.50 < r/d_hyd < 0.55
k_Re = 5.45/Re^(0.118) for 0.55 ≤ r/d_hyd < 0.70
k_Re = 11.5/Re^(0.19) for 0.70 ≤ r/d_hyd < 3.00Turbulent regime (Re ≥ 3e5) with independence of local resistance coefficient on Reynolds number
zeta_LOC = A1*B1*C1
with
A1 |
as coefficient considering effect of angle of turning (delta) [-], |
A2 |
as coefficient considering effect for laminar regime [-], |
B1 |
as coefficient considering effect of relative curvature radius (R_0/d_hyd) [-], |
C1=1 |
as coefficient considering relative elongation of cross sectional area (here: circular cross sectional area) [-], |
k_Re |
as coefficient considering influence of laminar regime in transition regime [-], |
Re |
as Reynolds number [-]. |
The pressure loss coefficient zeta_TOT of a curved bend including pressure loss due to friction is determined by its local resistance coefficient zeta_LOC multiplied with a correction factor CF for surface roughness according to [Miller, p. 209, eq. 9.4]:
zeta_TOT = CF*zeta_LOC
where the correction factor CF is determined from the Darcy friction factor of a straight pipe having the bend flow path length
CF = 1 + (lambda_FRI_rough * pi * delta/d_hyd) / zeta_LOC
and the Darcy friction factors lambda_FRI_rough is calculated with an approximated Colebrook-White law according to [Miller, p. 191, eq. 8.4]:
lambda_FRI_rough = 0.25*(lg(K/(3.7*d_hyd) + 5.74/Re^0.9))^-2
with
delta |
as curvature radiant [rad], |
d_hyd |
as hydraulic diameter [m], |
K |
as absolute roughness (average height of surface asperities) [m], |
lambda_FRI_rough |
as Darcy friction factor[-], |
Re |
as Reynolds number [m], |
zeta_LOC |
as local resistance coefficient [-], |
zeta_TOT |
as pressure loss coefficient [-]. |
The correction for surface roughness through CF is used only in the turbulent regime, where the fluid flow is influenced by surface asperities not covered by a laminar boundary layer. The turbulent regime starts at Re ≥ 4e4 according to [Idelchik 2006, p. 336, sec. 15]. There is no correction due to roughness in the laminar regime up to Re ≤ 6.5e3 according to [Idelchik 2006, p. 336, sec. 15].
Nevertheless the transition point from the laminar to the transition regime is shifted to smaller Reynolds numbers for an increasing absolute roughness. This effect is considered according to [Samoilenko in Idelchik 2006, p. 81, sec. 2-1-21] as:
Re_lam_leave = 754*exp(if k ≤ 0.007 then 0.0065/0.007 else 0.0065/k)
with
k = K /d_hyd |
as relative roughness [-], |
Re_lam_leave |
as Reynolds number for leaving laminar regime [-]. |
Note that the beginning of the laminar regime cannot be beneath Re ≤ 1e2 .
The pressure loss coefficient zeta_TOT of a curved bend in dependence of the Reynolds number Re for different relative curvature radii R_0/d_hyd and different angles of turning delta is shown in the figures below.
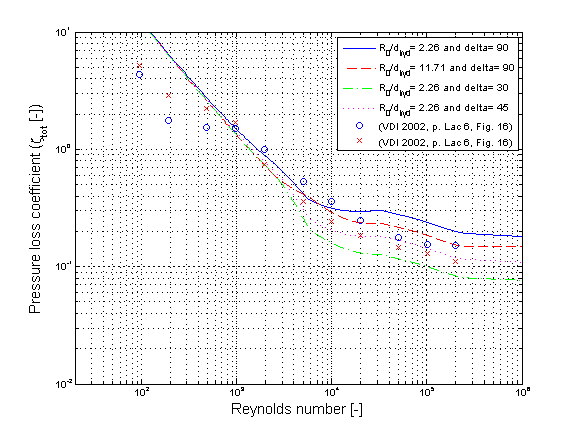
There are deviations of the pressure loss coefficient zeta_TOT comparing different references. Usually these deviations in the transition regime have to be accepted due to an uncertainty for the determination of comparable boundary conditions in the different references. Nevertheless these calculations cover the usual range of pressure loss coefficients for a curved bend. The pressure loss coefficient zeta_TOT for the same geometry can be adjusted via varying the average height of surface asperities K for calibration.
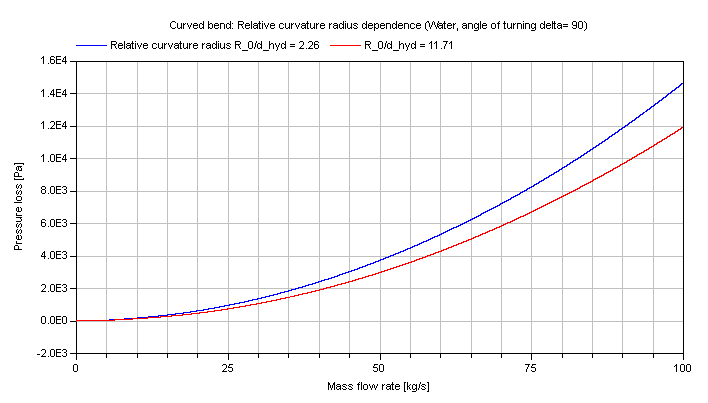
The pressure loss in dependence of the mass flow rate of water is shown for different relative curvature radii:
The pressure loss in dependence of the mass flow rate of water is shown for different angles of turning:
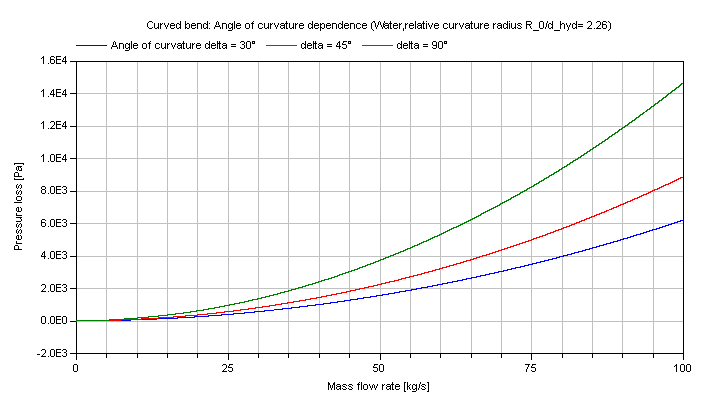
Note that there is a small deviation between the compressible and incompressible calculation due to the lack of a direct analytical invertibility.
Extends from Modelica.Icons.Information (Icon for general information packages).
 Class Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend.dp_edgedOverall
Class Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend.dp_edgedOverall
Calculation of pressure loss in edged bends with sharp corners at overall flow regime for incompressible and single-phase fluid flow through circular cross sectional area considering surface roughness.
This function shall be used inside of the restricted limits according to the referenced literature.
The pressure loss dp for edged bends is determined by:
dp = zeta_TOT * (rho/2) * velocity^2
with
| rho | as density of fluid [kg/m3], |
| velocity | as mean velocity [m/s], |
| zeta_TOT | as pressure loss coefficient [-]. |
The pressure loss coefficient zeta_TOT of an edged bend can be calculated for different angles of turning delta by:
zeta_TOT = A * C1 * zeta_LOC * CF_Fri* CF_Re [Idelchik 2006, p. 366, diag. 6-7] and [Miller 1984, p. 149, sec. 9.4]
with
| A | as coefficient considering effect for angle of turning [-], |
| C1 | as coefficient considering relative elongation of cross sectional area (here: circular cross sectional area) [-], |
| CF_Fri | as correction factor considering surface roughness [-], |
| CF_Re | as correction factor considering Reynolds number [-], |
| delta | as angle of turning [deg]. |
The correction factor CF_Fri regarding the influence of surface roughness is determined as ratio of the Darcy friction factor for rough surfaces to smooth surfaces according to [Miller, p. 207, eq. 9.3]:
CF_Fri = lambda_FRI_rough / lambda_FRI_smooth
and the Darcy friction factors lambda_FRI are calculated with an approximated Colebrook-White law according to [Miller, p. 191, eq. 8.4]:
lambda_FRI = 0.25*(lg(K/(3.7*d_hyd) + 5.74/Re^0.9))^-2
with
| d_hyd | as hydraulic diameter [m], |
| K | as absolute roughness (average height of surface asperities) [m], |
| lambda_FRI | as Darcy friction factor[-], |
| Re | as Reynolds number [m], |
| zeta_TOT | as pressure loss coefficient [-]. |
Note that the Darcy friction factor for a smooth surface lambda_FRI_smooth is calculated with the previous equation and an absolute roughness of K = 0 .
The correction for surface roughness through CF_Fri is used only in the turbulent regime, where the fluid flow is influenced by surface asperities not covered by a laminar boundary layer. Here the correction according to friction starts at Re ≥ Re_lam_leave according to [Idelchik 2006, p. 336, sec. 15]. Here the end of the laminar regime is restricted to a Reynolds number smaller than 2e3 w.r.t [VDI, p. Lac 6, fig. 16].
Nevertheless the transition point from the laminar to the transition regime is shifted to smaller Reynolds numbers for an increasing absolute roughness. This effect is considered according to [Samoilenko in Idelchik 2006, p. 81, sec. 2-1-21] as:
Re_lam_leave = 754*exp(if k ≤ 0.007 then 0.0065/0.007 else 0.0065/k)
with
| k = K /d_hyd | as relative roughness [-], |
| Re_lam_leave | as Reynolds number for leaving laminar regime [-]. |
Note that the beginning of the laminar regime cannot be beneath Re ≤ 5e2 .
In addition the influence or decreasing Reynolds numbers Re on the pressure loss coefficient zeta_TOT in the laminar and turbulent regime is considered through a second correction factor CF_Re according to [Miller 1984, p. 149, sec. 9.4] by:
CF_Re = B/Re^exp for Re ≤ 2e5
with
| B = f(Geometry) | as coefficient considering effect of Reynolds number in laminar regime [-], |
| exp | as exponent for Reynolds number in laminar regime [-], |
| Re | as Reynolds number [-], |
Note that the coefficient B considers the influence of the angle of turning delta on the pressure loss coefficient zeta_TOT in the laminar regime according to [Idelchik 2006, p. 340, sec. 28].
Note that the correction of the pressure loss coefficient zeta_TOT is influenced by the correction factor CF_Re only for decreasing Reynolds numbers Re out of the turbulent fluid flow regime at Re ≤ 2e5 into transition and laminar fluid flow regime.
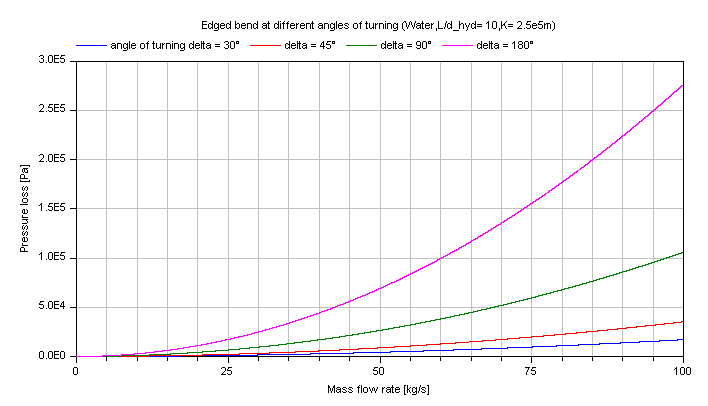
The pressure loss coefficient zeta_TOT of a edged bend in dependence of the Reynolds number Re for different angles of turning delta is shown in the figures below.

Pressure loss calculation of edged bends is complex and there are large differences in literature data. Nevertheless these calculations cover the usual range of pressure loss coefficients for an edged bend.
The validation of the pressure loss coefficient for an edged bends shows four possible flow regimes:
Incompressible case [Pressure loss = f(m_flow)]:
The pressure loss in dependence of the mass flow rate of water is shown for different angles of turning:
Compressible case [Mass flow rate = f(dp)]:
The mass flow rate in dependence of the pressure loss of water is shown for different angles of turning:

Extends from Modelica.Icons.Information (Icon for general information packages).