 Package HydraulicsByFluidon.Components.Volumes
Package HydraulicsByFluidon.Components.VolumesIcon for standard packages
 Package HydraulicsByFluidon.Components.Volumes
Package HydraulicsByFluidon.Components.Volumes
Standard package icon.
Extends from Modelica.Icons.Package (Icon for standard packages).
| Name | Description |
|---|---|
BladderAccumulator | |
OpenTank | |
PistonAccumulator | |
Volume | |
VolumeExt |
 Model HydraulicsByFluidon.Components.Volumes.BladderAccumulator
Model HydraulicsByFluidon.Components.Volumes.BladderAccumulator
Model of a gas-loaded accumulator with a bladder separating the media. Fluid inertia or the stiffness of the bladder is not considered. The gas is modelled as an ideal gas.
The parameters Biasing pressure, Nominal volume and Dead volume describe the accumulator in the unconnected state. At the beginning of a simulation, the state variables of the accumulator are computed depending on the parameter Initial pressure of the hydraulic volume and Isothermal start.
If the bladder expands to its maximum volume, only the Dead volume remains in the accumulator. Due to the typically small dead volume, a high mathematical stiffness of the accumulator can result. This behavior might require choosing a correspondingly small timestep.
The parameter Polytropic exponent characterizes how pressure changes affect the volume and stiffness of the gas bladder. If Polytropic exponent is set to unity, the change of state within the gas is isothermal. This implies perfect heat transfer between the gas in the bladder and the environment such that no change of temperature occurs in the gas. This situation is encountered in hydraulic accumulators if the load cycles of the liquid are lengthy.
If the Polytropic exponent is set to the isentropic exponent (1.4 for air), the gas undergoes an adiabatic change of state which means that no heat exchange with the environment can occur. This is typically the case for very short load cycles.
If Isothermal start is set to true, it is assumed that the change from biasing pressure to the initial pressure happened at constant temperature. If Isothermal start is set to false, a polytropic process incorporating the parameter Polytropic exponent is assumed.
| Type | Name | Default | Description |
|---|---|---|---|
Volume | nominalVolume | 0.005 | Nominal volume |
Volume | deadVolume | 1e-4 | Dead volume |
AbsolutePressure | relBiasingPressure | 5e+6 | Biasing pressure (rel.) |
Temperature | biasingTemperature | 293.1 | Biasing Temperature |
Real | polytropicExponent | 1.4 | Polytropic exponent |
Boolean | isothermalStart | true | Isothermal start |
AbsolutePressure | initialPressure | environment.pAmbient | Initial pressure of the hydraulic volume |
Boolean | FixedInitialPressure | false | fixed initial pressure |
Boolean | enableVolumeOutput | false | Enable fluid volume output |
| Type | Name | Description |
|---|---|---|
FluidPort | fluidPort | Hydraulic port |
output RealOutput | fluidVolume | Fluid volume |
 Model HydraulicsByFluidon.Components.Volumes.PistonAccumulator
Model HydraulicsByFluidon.Components.Volumes.PistonAccumulator
Model of a gas-loaded accumulator with a piston separating the media. Fluid inertia is not considered. The gas is modelled as an ideal gas.
The parameters Biasing pressure, Nominal volume, Dead volume, and Additional gas volume describe the accumulator in the unconnected state.
At a piston stroke of 0 m only the Dead volume remains in the accumulator. Due to the typically small dead volume, a high mathematical stiffness of the accumulator can result. This behavior might require choosing a correspondingly small timestep.
The parameter Polytropic exponent characterizes how pressure changes affect the volume and stiffness of the gas volume. If Polytropic exponent is set to unity, the change of state within the gas is isothermal. This implies perfect heat transfer between the gas in the bladder and the environment such that no change of temperature occurs in the gas. This situation is encountered in hydraulic accumulators if the load cycles of the liquid are lengthy.
If the Polytropic exponent is set to the isentropic exponent (1.4 for air), the gas undergoes an adiabatic change of state which means that no heat exchange with the environment can occur. This is typically the case for very short load cycles.
The Biasing pressure (rel.) is converted according to the ratio of Biasing Temperature and fluid temperature and the Polytropic exponent at the beginning of the simulation.
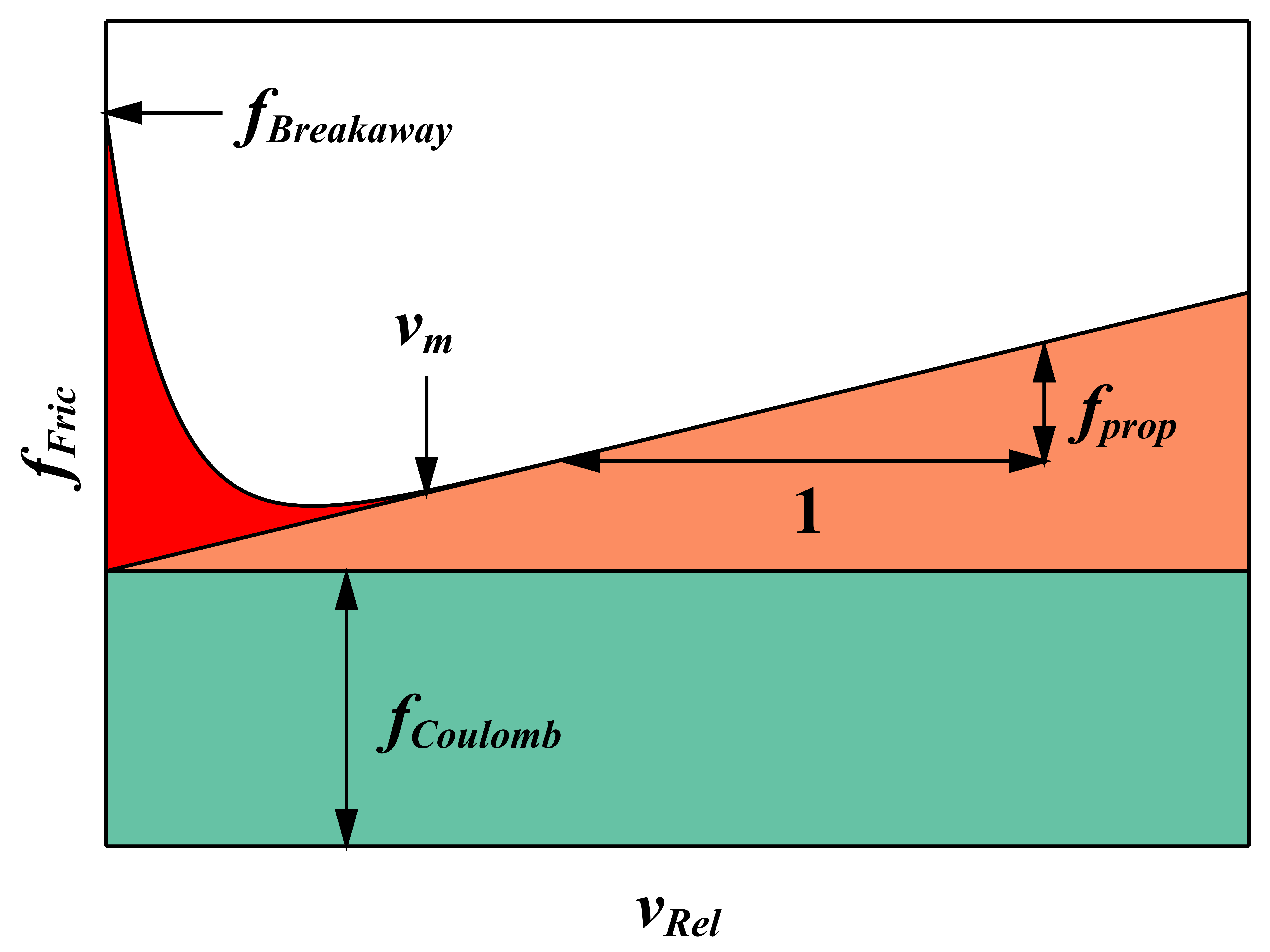
The parameters Breakaway friction force, Constant friction/Coulomb force, Velocity dependent friction and Velocity parameter for Stribeck friction (velocity where the friction force begins to grow linearly) characterize the velocity dependence of the friction force between piston and cylinder.
| Type | Name | Default | Description |
|---|---|---|---|
Length | pistonDiameter | 0.2 | Diameter of piston |
Volume | nominalVolume | 0.005 | Nominal volume |
Volume | gasDeadVolume | 5e-4 | Additional gas volume |
Volume | deadVolume | 1e-4 | Fluid dead volume |
Angle | angle | 0 | Inclination angle |
Mass | massPiston | 1 | Piston mass |
Pressure | relBiasingPressure | 5e+6 | Biasing pressure (rel.) |
Temperature | biasingTemperature | 293.1 | Biasing Temperature |
Real | polytropicExponent | 1.4 | Polytropic exponent |
Real | fProp | 10000 | Velocity dependent friction |
Force | fCoulomb | 25 | Constant friction/Coulomb force |
Force | fBreakaway | 50 | Breakaway friction force |
Velocity | vM | 0.005 | Velocity parameter for Stribeck friction |
Boolean | enableStrokeOutput | false | Enable stroke output |
Boolean | enableVelocityOutput | false | Enable velocity output |
Boolean | enableVolumeOutput | false | Enable fluid volume output |
| Type | Name | Description |
|---|---|---|
FluidPort | fluidPort | Hydraulic port |
output RealOutput | strokeOut | Stroke of piston |
output RealOutput | velocityOut | Velocity of piston |
output RealOutput | volumeOut | Fluid volume |
 Model HydraulicsByFluidon.Components.Volumes.Volume
Model HydraulicsByFluidon.Components.Volumes.Volume
Model of a simple hydraulic capacity. It can be used to represent the volume of adjacent components that lack any spatial expansion, e. g. the IdealResistor component. The temporal change rate of pressure equals the net mass flow into the capacity.
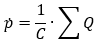
The capacity C used to calculate the rate of pressure change takes into account the compression modulus of the fluid. The housing is assumed to be ideally rigid (in comparison to fluid). If the housing is to be taken into account, component VolumeExt must be used.
| Type | Name | Default | Description |
|---|---|---|---|
Volume | capacity | 0.001 | Size of the volume |
| Type | Name | Description |
|---|---|---|
FluidPort | fluidPort | Hydraulic port |
 Model HydraulicsByFluidon.Components.Volumes.VolumeExt
Model HydraulicsByFluidon.Components.Volumes.VolumeExt
Model of a simple hydraulic capacity with consideration of surrounding housing. It can be used to represent the volume of adjacent components that lack any spatial expansion, e. g. the IdealResistor component. The temporal change rate of pressure equals the net mass flow into the capacity.
| Type | Name | Default | Description |
|---|---|---|---|
Volume | capacity | 0.001 | Size of the volume |
BulkModulus | bulkModulus | 2.1e+11 | Bulk modulus housing |
| Type | Name | Description |
|---|---|---|
FluidPort | fluidPort | Hydraulic port |
 Model HydraulicsByFluidon.Components.Volumes.OpenTank
Model HydraulicsByFluidon.Components.Volumes.OpenTank
The OpenTank component is the model of an open tank with unlimited volume in the sense of a line termination. The pressure at fluidPort can either be set to environment.pAmbient pressure or a different pressure.
| Type | Name | Default | Description |
|---|---|---|---|
Boolean | useEnvironmentPressure | true | Pressure at the fluid port equals environment.pAmbient |
AbsolutePressure | pressure | environment.pAmbient | Pressure at the fluid port if useAmbientPressure = false |
| Type | Name | Description |
|---|---|---|
FluidPort | fluidPort | Hydraulic port |