Both single phase surface tension and adhesion modeling is based on the work of
Akinci et al.
Both models are capable of reproducing qualitatively realistic results, but are in
principle unphysical and cannot be generalized for an arbitrary case/simulation.
Because of this, trial-and-error tuning of the surface tension coefficient and the
adhesion coefficient is necessary if realistic fluid behavior is to be achieved.
Both adhesion and single phase surface tension models rely on a form inter-particle
force, which binds the particles together. The way the force is modeled is through a
specific kernel shape which mimics a potential energy well. In that sense, particles
tend to keep a certain distance from each other and introduce elastic forcing if the
particles get too close or too far from each other.
The equation that dictates the adhesion force is given by:
Figure 1 .
F
a d
= −
∑
n b r s
β
m
i
W
A k
V
i
Δ
x
i j
|
Δ
x
i j
|
While the single phase surface tension is defined by:
Figure 2 .
F
c o h
= −
∑
n b r s
2
ρ
0
ρ
i
+
ρ
j
γ
m
i
2
W
C o h
Δ
x
i j
|
Δ
x
i j
|
Where,
Indicies
A
d
C
o
h
W
m
Δ
x
i
j
ρ
i
ρ
j
ρ
o
β
γ
The
β
parameter is specified for each
WALL or
MOVINGWALL phase. That means that the
level of adhesion can be different for every
WALL or
MOVINGWALL phase. The same applies to the
γ
value for the surface tension forces. The balance
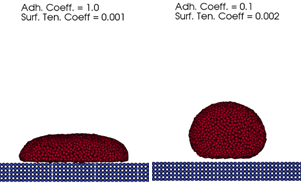
between surface tension and adhesion forces can replicate qualitatively the physical
contact angles between the fluid and the solid elements. An example of balancing
adhesion and surface tension forces is shown in
Figure 1 .
Figure 3 . Single phase fluid droplet on a plate . Using different values of the adhesion and surface tension coefficient
produces effects of different contact angles. The adhesion model can be used in conjunction with the more physical multiphase
surface tension model. In that situation, the surface tension forces are physical
and only the adhesion model is left to be tuned, which can be a significantly easier
exercise.
Modeling Physical Behavior of Single Phase Surface Tension and Adhesion
The nanoFluidX team has performed a number of tests
resulting in the development of consistent single phase surface tension and adhesion
behavior. By consistency it is meant that if appropriate/desired behavior is found
for a given resolution and a given surface tension or adhesion coefficient such
behavior can be replicated for other resolutions by following the below
methodology.
The simulation data show that the variations of surface tension coefficient
σ
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaeq4Wdmhaaa@37CC@
ϵ
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamrr1ngBPrwtHr
hAXaqeguuDJXwAKbstHrhAG8KBLbacfiaeaaaaaaaaa8qacqWF1pG8 aaa@4204@
d
x
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamizaiaadIhaaaa@37EF@
α
d
x
−
β
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqySdeMaamizaiaadIhapaWaaWbaaSqabeaapeGaeyOeI0IaeqOS
digaaaaa@3C68@
α
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqySdegaaa@37A8@
β
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqOSdigaaa@37AA@
β
=
0.7
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqOSdiMaeyypa0JaaGimaiaac6cacaaI3aGaaiiOaaaa@3C01@
0.95
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaaGimaiaac6cacaaI5aGaaGynaaaa@38F7@
The procedure to obtain new
σ
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaeq4Wdmhaaa@37CC@
or when
d
x
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamizaiaadIhaaaa@37EF@
changes is as follows:
Assume your current values are
d
x
c
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamizaiaadIhapaWaaSbaaSqaa8qacaWGJbaapaqabaaaaa@3931@
σ
c
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaeq4Wdm3damaaBaaaleaapeGaam4yaaWdaeqaaaaa@390E@
ϵ
c
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamrr1ngBPrwtHr
hAXaqeguuDJXwAKbstHrhAG8KBLbacfiaeaaaaaaaaa8qacqWF1pG8
paWaaSbaaSqaa8qacaWGJbaapaqabaaaaa@4346@
You have a new
d
x
n
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamizaiaadIhapaWaaSbaaSqaa8qacaWGUbaapaqabaaaaa@393C@
σ
n
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaeq4Wdm3damaaBaaaleaapeGaamOBaaWdaeqaaaaa@3919@
ϵ
n
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamrr1ngBPrwtHr
hAXaqeguuDJXwAKbstHrhAG8KBLbacfiaeaaaaaaaaa8qacqWF1pG8
paWaaSbaaSqaa8qacaWGUbaapaqabaaaaa@4351@
Set
β
=
0.7
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqOSdiMaeyypa0JaaGimaiaac6cacaaI3aGaaiiOaaaa@3C01@
β
=
0.95
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqOSdiMaeyypa0JaaGimaiaac6cacaaI5aGaaGynaiaacckaaaa@3CC2@
Use
d
x
c
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamizaiaadIhapaWaaSbaaSqaa8qacaWGJbaapaqabaaaaa@3931@
σ
c
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaeq4Wdm3damaaBaaaleaapeGaam4yaaWdaeqaaaaa@390E@
ϵ
c
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamrr1ngBPrwtHr
hAXaqeguuDJXwAKbstHrhAG8KBLbacfiaeaaaaaaaaa8qacqWF1pG8
paWaaSbaaSqaa8qacaWGJbaapaqabaaaaa@4346@
α
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqySdegaaa@37A8@
For example:
Figure 4 .
α
=
σ
c
d
x
c
0.7
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqySdeMaeyypa0ZaaSaaa8aabaWdbiabeo8aZ9aadaWgaaWcbaWd
biaadogaa8aabeaaaOqaa8qacaWGKbGaamiEa8aadaqhaaWcbaWdbi
aadogaa8aabaWdbiaaicdacaGGUaGaaG4naaaaaaaaaa@4162@
or
Figure 5 .
α
=
ϵ
c
d
x
c
0.95
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqySdeMaeyypa0ZaaSaaa8aabaWefv3ySLgznfgDOfdaryqr1ngB
PrginfgDObYtUvgaiuGapeGae8x9di=damaaBaaaleaapeGaam4yaa
WdaeqaaaGcbaWdbiaadsgacaWG4bWdamaaDaaaleaapeGaam4yaaWd
aeaapeGaaGimaiaac6cacaaI5aGaaGynaaaaaaaaaa@4C5B@
Use the
α
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqySdegaaa@37A8@
σ
n
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaeq4Wdm3damaaBaaaleaapeGaamOBaaWdaeqaaaaa@3919@
ϵ
n
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamrr1ngBPrwtHr
hAXaqeguuDJXwAKbstHrhAG8KBLbacfiaeaaaaaaaaa8qacqWF1pG8
paWaaSbaaSqaa8qacaWGUbaapaqabaaaaa@4351@
For example,
Figure 6 .
σ
n
=
α
d
x
n
0.7
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaeq4Wdm3damaaBaaaleaapeGaamOBaaWdaeqaaOWdbiabg2da9iab
eg7aHjaadsgacaWG4bWdamaaDaaaleaapeGaamOBaaWdaeaapeGaaG
imaiaac6cacaaI3aaaaaaa@4149@
or
Figure 7 .
ϵ
n
=
α
d
x
n
0.95
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamrr1ngBPrwtHr
hAXaqeguuDJXwAKbstHrhAG8KBLbacfiaeaaaaaaaaa8qacqWF1pG8
paWaaSbaaSqaa8qacaWGUbaapaqabaGcpeGaeyypa0JaeqySdeMaam
izaiaadIhapaWaa0baaSqaa8qacaWGUbaapaqaa8qacaaIWaGaaiOl
aiaaiMdacaaI1aaaaaaa@4C42@
These approximations are to save time when you want to change
d
x
MathType@MTEF@5@5@+=
feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamizaiaadIhaaaa@37EF@