Discrete time system simulation

You can simulate models of discrete time systems using unitDelay, transferFunction, and stateSpace blocks. These discrete blocks have built-in samplers on their inputs and zero-order holds on their outputs.

You set the sample time of a transferFunction and stateSpace blocks in the dT parameters of their Properties dialogs. The dT parameter sets the sample time at which the blocks’ states are updated. The unitDelay block has a Boolean clock at its input to set the sample time.

Simulating multi-rate systems: Discrete time systems in Embed can be formulated as multi-rate systems. This means that a single model can contain blocks with different sampling rates. This capability is particularly useful in the simulation of discrete Multiple-Input-Multiple-Output (MIMO) systems. For a system with significant differences in its time constants in some natural modes or control loops, you can achieve improved performance by sampling different subsystems at different rates.

To specify multi-rate subsystems, use different sample times in the corresponding discrete transferFunction or discrete stateSpace blocks. The simulation time step must be set to a value equal to or less than the smallest value of all the sample times used in the discrete blocks.

Entering difference equations

A difference equation is like an ordinary differential equation, but instead of continuous functions, functions in a difference equation take on values only at discrete instances of time. Just as the operator in an ordinary differential equation is the integrator, the operator in the difference equation is the unit delay.

To understand how to represent a difference equation in block diagram form, consider the following example of the trapezoidal integration algorithm in difference equation form:

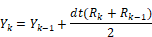
where:

R = input

Y = output

Here, dt is the fixed discrete update time and the subscript k and k-1 denote time in integer multiples of dt. Thus:

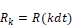
and

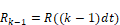
A DE is converted to a transfer function in terms of the Z operator by replacing occurrences of:

with

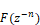
Thus:

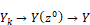
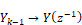
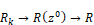
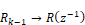
Performing the replacement and solving for Y/R yields:

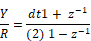
Since transfer functions are conventionally expressed in positive powers of z, you must multiply the right-hand side of the equation by z/z to produce:

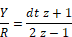
The procedure to create a block diagram is similar to the one used for continuous time transfer functions; however, the unitDelay block replaces the integrator block. The resulting block diagram becomes:

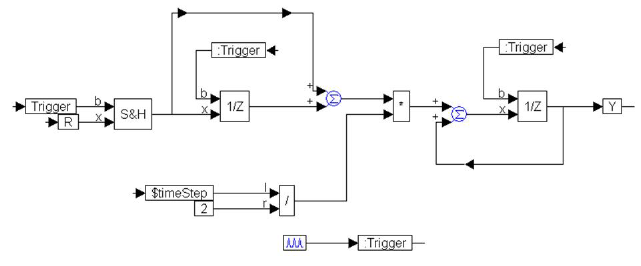
The continuous input signal, R, is made a discrete function by passing it through a sampleHold block to effectively sample and hold its value every time the trigger is activated. The trigger is activated every dt sec using the pulseTrain block, and must be fed into every unitDelay block to synchronize the Embed data flow.