ode113
Solve a system of non-stiff differential equations.
Syntax
[t,y] = ode113(@func,tin,y0)
[t,y] = ode113(@func,tin,y0,options)
[t,y,te,ye,ie] = ode113(...)
Inputs
- func
- The system of equations to solve.
- tin
- The vector of times (or other domain variable) at which to report the solution. If the vector has two elements, the solver operates in single step mode and determines appropriate intermediate steps.
- y0
- The vector of initial conditions.
- options
- A struct containing options settings specified via odeset.
Outputs
- t
- The times at which the solution is computed.
- y
- The solution matrix, with the solution at each time stored by row.
- te
- The index of the event that recorded each zero value.
- ye
- The system function values corresponding to each te value.
- ie
- The event index corresponding to each zero value.
Example
Find the transient current in a series RLC circuit.
function dy = RLC(t,y,R,L,C)
% y = [i, di/dt]
dy = [0, 0];
dy(1) = y(2);
dy(2) = -y(1)/(L*C) - y(2)*(R/L);
end
v = 2.4; % volts
R = 1.1; % resistor
L = 1.6; % inductor
C = 0.8; % capacitor
handle = @(t,y) RLC(t,y,R,L,C);
t = [0:0.2:12]; % time vector
yi = [0, v/L];
[t,y] = ode113(handle,t,yi);
a = y(:,1)';
plot(t,a);
xlabel('time');
ylabel('amplitude');
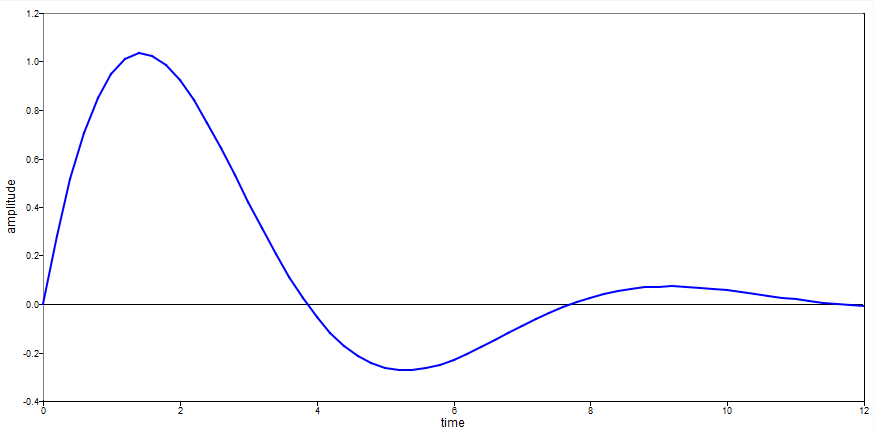
Figure 1. chirp figure 1
Comments
ode113 solves the system using the Adams method algorithm from the Sundials CVODE library.
To pass additional parameters to a function argument, use an anonymous function.
- RelTol: 1.0e-3
- AbsTol: 1.0e-6
The 'Events' function used with the last three output arguments is specified using odeset.