HS-5020: Stochastic Study of a Cantilever I-beam
In this tutorial, you will complete a simple Stochastic study to investigate uncertain parameters of a cantilever I-beam model defined with four variables and four functions.

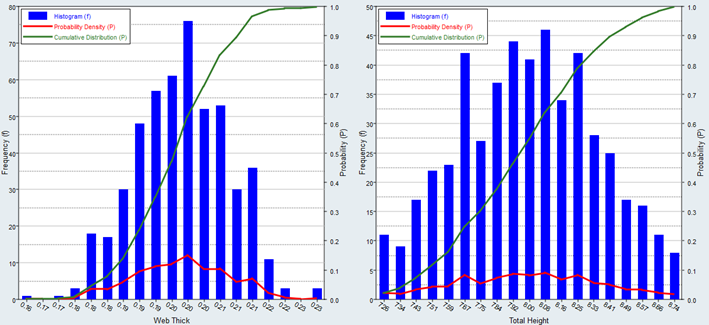
Figure 1.
Run a Stochastic Study
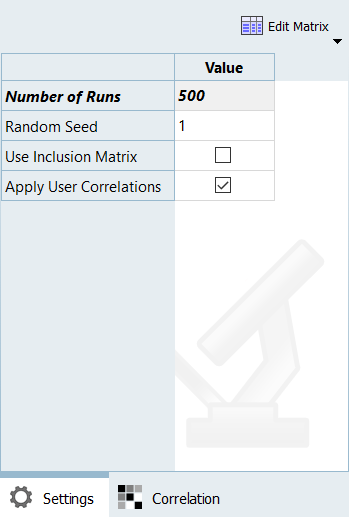
In this step, you will run a Stochastic study and review the evaluation scatter.
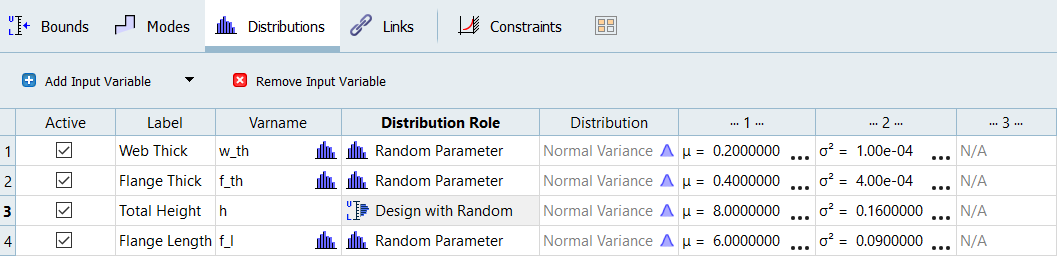
In this study, you will consider w_th, f_l and f_th as Random parameters (uncertain, not controllable by design) and h as Design with Random parameter (uncertain but controllable by design).
Review Post-Processing Results
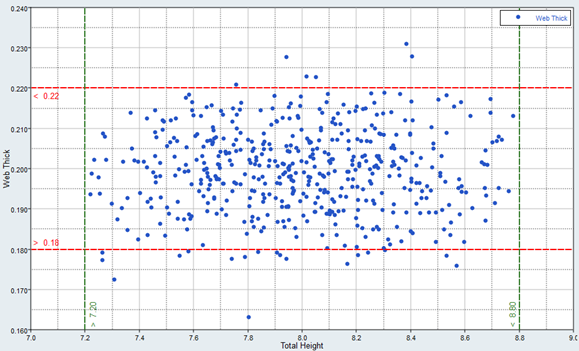
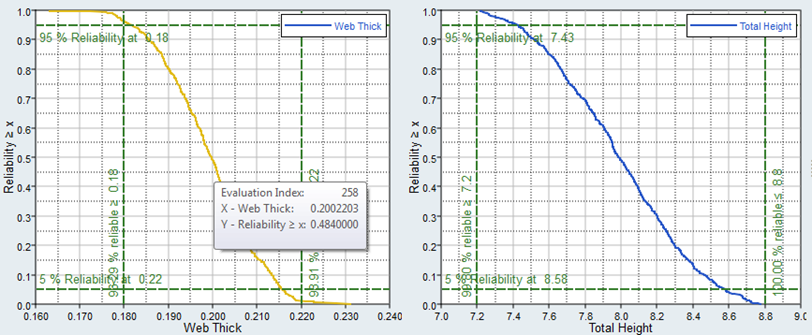
In this step, you will review the evaluation results within the Post-Processing step.