Maxwell's equations for magnetic systems
Introduction
Maxwell's equations are the fundamental laws of electromagnetism.
They relate the density of the electrical charges q and the density of the
electrical current ![]() in a
domain to the fields which result from it:
in a
domain to the fields which result from it:
- the
electrical field strength
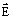 and the electrical
flux density
and the electrical
flux density 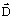
- the magnetic flux density
 and the
magnetic field strength
and the
magnetic field strength 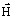
General form
The general form of Maxwell's equations is the following:
Maxwell-Gauss: ![]() (1)
(1)
Maxwell-Faraday: ![]() (2)
(2)
Gauss law for magnetism: ![]() (3)
(3)
Maxwell-Ampère: ![]() (4)
(4)
Other equations
The following constitutive laws of materials are added to the previous equations:
Characteristics of the conducting media: ![]() (5)
(5)
Characteristics of the magnetic media: ![]() (6)
(6)
Characteristics of the dielectrical media: ![]() (7)
(7)
where:
- σ is the conductivity of the material (in S)
- μ is the permeability (in H/m)
- ε is the permittivity (in F/m)
Separation
In the case of low frequency , the equations of
the electrical fields ![]() and
and ![]() and the
equations of the magnetic fields
and the
equations of the magnetic fields ![]() and
and ![]() can be
decoupled.
can be
decoupled.
Thus, there are Maxwell's equations for the electrical systems and Maxwell's equations for the magnetic systems, respectively:
- a set of equations for the electrical fields , and
- another set of equations for the magnetic fields.
This separation depends on materials, frequency, and on the dimension of the study domain. The decoupling of Maxwell equations in AC applications is usually possible for those technical devices working in the range of frequency f < 1 to 10 GHz.
Form of Maxwell equations for a magnetic system
For a magnetic system , we use the hypothesis of the quasi-static state and we neglect
the time variation of the electric flux density D (the displacement currents are
neglected). The hypothesis of quasi-static state remains true as long as the frequency
does not exceed a certain limit. This results in the null value of the term ![]() in equation 4.
in equation 4.
Thus, the equations can be written in the following way:
Maxwell-Faraday: ![]() (2)
(2)
Gauss law for magnetism: ![]() (3)
(3)
Maxwell-Ampere: ![]() (4)
(4)
Characteristic of the conducting media: ![]() (5)
(5)
Characteristic of the magnetic media: ![]() (6)
(6)