Maxwell's equations for electrical systems
Introduction
Maxwell's equations are the fundamental laws of electromagnetism.
They relate the density of the electric charges q and the density of the electric
current ![]() in a domain to
the fields which result from them:
in a domain to
the fields which result from them:
- the
electric field strength
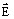 and the electric flux
density
and the electric flux
density 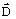
- the
magnetic flux density
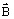 and the magnetic
field strength
and the magnetic
field strength 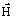
General form of the equations
The general form of Maxwell's equations in domains without moving bodies is the following:
Maxwell-Gauss : ![]() (1)
(1)
Maxwell-Faraday : ![]() (2)
(2)
Conservation of magnetic flux density : ![]() (3)
(3)
Maxwell-Ampere: ![]() (4)
(4)
Other equations
With these equations, the following constitutive laws of materials are added:
Characteristics of the conducting media : ![]() (5)
(5)
Characteristics of the magnetic media : ![]() (6)
(6)
Characteristics of the dielectric media : ![]() (7)
(7)
where :
- σ is the conductivity of the material (in S)
- μ is the permeability (in H/m)
- ε is the permittivity (in F/m)
Separation
In the case of low frequency AC fields , the
equations in the electric fields ![]() and
and ![]() and the
equations of the magnetic fields
and the
equations of the magnetic fields ![]() and
and ![]() can be
decoupled.
can be
decoupled.
Thus, there are Maxwell's equations for the electrical systems and Maxwell's equations for the magnetic systems, respectively:
- a set of equations for the electric fields, and
- another set of equations for the magnetic fields.
This separation of the electrical and magnetic systems depends on: materials, work frequencies, size of the study domain. It is usually possible for technical devices working in the range of frequency f < 1 to 10 GHz.
Form of equations for an electrical system
For an electrical system, we suppose that the
magnetic field do es not modify the current distribution ![]() in the conductors. This assumption remains true as
long as the frequency does not exceed a certain limit. This results
in the null value of the term
in the conductors. This assumption remains true as
long as the frequency does not exceed a certain limit. This results
in the null value of the term ![]() in equation (2).
in equation (2).
Thus, the equation can be written in the following way:
Maxwell-Gauss : ![]() (1)
(1)
Maxwell-Faraday : ![]() (2)
(2)
Maxwell-Ampere : ![]() (4)
(4)
Characteristic of the conducting media : ![]() (5)
(5)
Characteristic of the dielectric media : ![]() (7)
(7)