Basic definitions: magnetic flux, inductance,...
Magnetic flux: definition
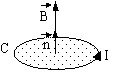
Let there be a filiform circuit closed-loop, defined by its contour C and provided with an electric current I.
The magnetic flux Φ associated with the contour C is defined by:
(1)
where:
-
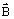is the magnetic field created by the current I -
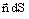is the vector element of surface
Stokes' theorem expresses the magnetic flux as a line integral, in the following form:
where:
-
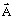is the magnetic vector potential (such as 
) -
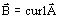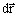is the vector element of line
Inductance: definition
The inductance of a filiform circuit closed-loop, defined by its contour C and provided with an electric current I, is defined by the formula:
It can be expressed by one of the two following formulas:
Self-inductance and mutual inductance
Let i and j be two filiform circuit closed-loops, defined by their contour Ci and Cj and flowed through by the electric currents Ii and Ij.
The mutual inductance between i and j circuits is defined by the formula:
where Φij is the magnetic flux through the closed-loop Cj generated by the magnetic field produced exclusively by the current Ii.
With respect to this last definition, the self-inductance of the closed-loop Ci corresponds to the particular case where i = j:
