The Hydrodynamic Lubrication Model
The model integrates the work of three studies, resulting in a model that may be used for both particle-particle and particle-geometry contacts, with the assumption that the system is fully saturated, and no fluid free-surface is involved.
The model is most useful when modeling dense granular suspensions, where shear and extensional flow effects are important, but it might be applied to simulate any saturated system where short-range hydrodynamic forces are important. Because the model's intended application is for small particles (e.g., millimetre or micron-sized), it is less relevant to large particles (e.g., rocks), though the model's applicability limits are currently unclear.
Calculating Particle-Particle Force and Torque
For particle-particle contacts the model uses the theory as outlined in the work of Cheal & Ness (2018) .
In Figure 1, for two particles p1 and p2 with linear velocities U1 and U2, rotating at angular velocities Ω1 and Ω2, with center-center vector d, pointing from p2 to p1, with corresponding unit normal n=d/|d|, the force F and torque Γ acting on p1 are defined as:
![]()
![]()
where ⊗ is the outer product, μ is the viscosity of the fluid, and the remaining coefficients are defined as:
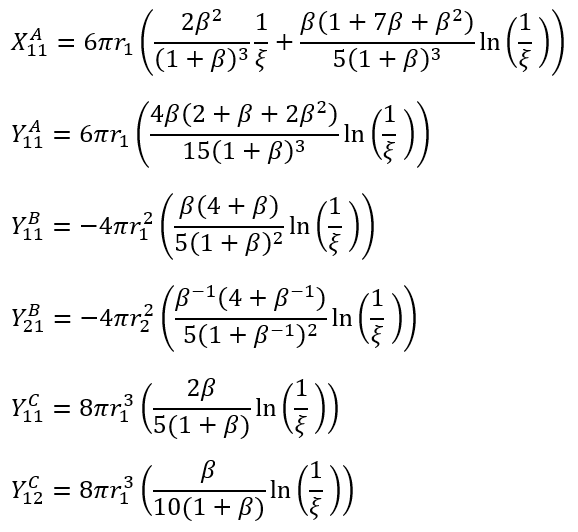
where
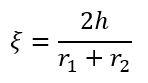
![]()
As mentioned in Cheal & Ness (2018) , the model is only intended to capture ‘short range contributions’. Therefore, interactions are only considered if they satisfy the following outer cutoff condition:
![]()
where rmin is the smallest of the two particle radii:
![]()
In addition to this condition, an additional inner cutoff condition is imposed so that the lubrication forces and torques are calculated down to a minimum separate distance of 0.001 rmin.
For contacts that have h < 0.001 rmin, the following is applied:
![]()
so that all forces and torques are only calculated in the range:
![]()
This additional condition is employed by following the approach of Cabiscol et al. (2021) .

Calculating Particle-Geometry Force and Torque
The works of two sets of authors are used for resolving particle-geometry contacts - one for calculating the normal force component (Goddard et al. (2020)) and the other for calculating the tangential force and torque components (O'Neil & Stewartson (1967)).
Normal Force
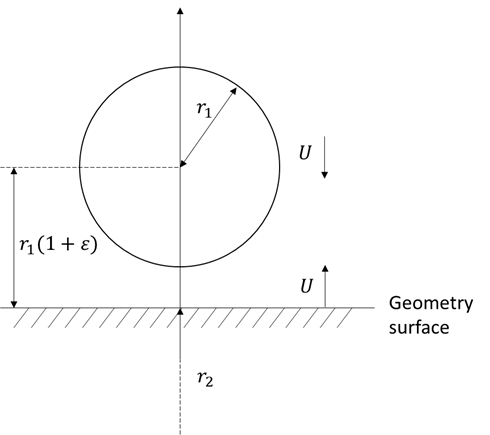
Following the approach of Goddard et al. (2020), for a particle of radius r1 approaching a geometry element with an assumed radius r2, that is very large, the ratio of their radii is defined as:
![]()
The gap between the particle and geometry is termed ε, which is non-dimensionalized by the particle radius as shown in the following figure.
The non-dimensional normal force on the particle as it approaches the geometry in the normal direction is then calculated by:
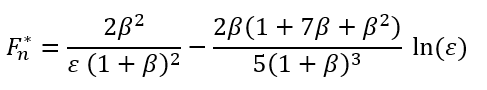
where higher order terms have been ignored.
Considering that the radius of the geometry element is assumed to be quite large, the resulting force experienced by the particle after re-dimensionalization with the typical drag scale 6πμUr1 is defined as:
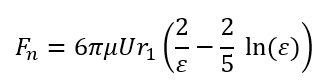
where 2U is the relative approach velocity between the particle and geometry and μ is the fluid viscosity.
Tangential Force and Torque
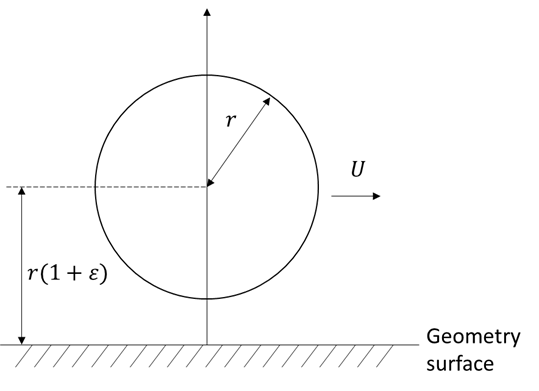
Following the approach of O’Neil & Stewartson (1967), consider the scenario of a particle of radius r moving parallel to a geometry. The non-dimensional gap between the particle and geometry is termed ε, as outlined previously and shown in the following figure.
The tangential force exerted on the particle is then defined as:
![]()
where
![]()
and the higher order terms in ε have been ignored. An equal and opposite force is applied to the geometry.
The torque applied is defined as:
![]()
where, for the particle:
![]()
and for the geometry:
![]()
The higher order terms in ε have been ignored.
Cutoffs
The inner and outer cutoffs explained previously for particle-particle contacts (and in Cabiscol et al. (2021) ) are also utilized for particle-geometry interactions, which means that the forces and torques outlined below are only ever applied in the range:
![]()
where h and rmin are as described previously.
Using the Hydrodynamic Lubrication Model
To use the Hydrodynamic Lubrication Model, you must first add it to the Physics of a given EDEM simulation and then configure as required.
- In the Creator Tree, select Physics.
- Select Particle to Particle and/or Particle to Geometry from the Interaction dropdown list.
- Click Edit Contact Chain at the lower section of the Physics panel.
- Under Plug-in Models, select the HydrodynamicLubrication checkbox.
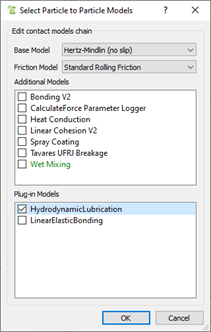
- Click OK.
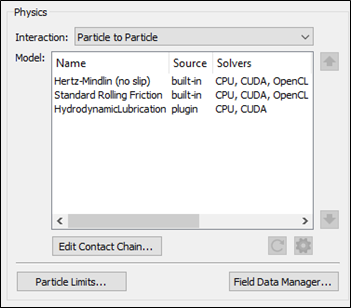
The plug-in is displayed in the Model panel. - Select the plug-in and click the
 icon in the lower-right section of the Physics panel to configure it.
icon in the lower-right section of the Physics panel to configure it.
The Hydrodynamic Lubrication Model Parameter Editor is displayed. - Specify the values for Fluid Viscosity, Inner Cutoff, and Outer Cutoff.
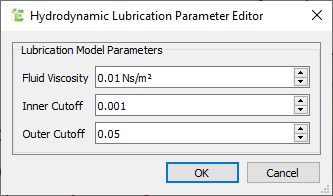
The Inner and Outer Cutoff values correspond to the non-dimensional values (by particle radius) between which the additional forces and torques are calculated. (For more information about specifying cutoff values, see Cabiscol et al. (2021)).Because one of the assumptions for the theory is that the particles are fully saturated with fluid, these values are applied to all particles in the simulation, rather than by type or interaction. - After specifying the values, click OK.
Post Processing
Lubrication forces and torques are directly added to the particle characteristics Total Force and Total Torque. As a result, they are difficult to analyze separately from other contact forces and torques.
(c) 2023 Altair Engineering Inc. All Rights Reserved.