Stdevp
The Population Standard Deviation of the selection.
The Stdevp deals with the complete population whereas Stdev deals with a population sample only.
The formula:
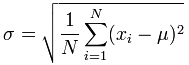
Sample 1
Population: A set of data that is all inclusive.
Populations are often very large. For simplicity, imagine the following as an example:
12,6,12
Compute the Stdevp:
- Determine the mean of the sample
12+6+12/3=10
- Square the difference between each item and the mean
(12-10)^2 =4
(6-10)^2 =16
(12-10)^2 =4 - Calculate the average
4+16+4/3=24/3
- Calculate the square root
√8 or 2.8284
Sample 2
Given the following sample fields:
| Number | Arbitrary | Negative Values | Positive Values | One | Binary | Currency | Decimal |
| 1 | 3 | -1 | 1 | 1 | 0 | $1.00 | 1.01 |
| 2 | 2 | -2 | 2 | 1 | $10.00 | 2.02 | |
| 3 | 1 | -3 | 3 | 0 | $100.00 | 3.03 | |
| 4 | 0 | -4 | 4 | 1 | $1,000.00 | 4.04 | |
| 5 | -1 | -5 | 5 | 0 | $10,000.00 | 5.05 | |
| 6 | -2 | -6 | 6 | 1 | -$1.00 | 6.06 | |
| 7 | -3 | -7 | 7 | 0 | -$10.00 | 7.07 | |
| 8 | 0 | -8 | 8 | -$100.00 | 8.08 | ||
| 9 | 0 | -9 | 9 | -$1,000.00 | 9.09 | ||
| 10 | 0 | -10 | 0 | $0.00 | 0.00 |
Sample fields
The Stdevp for each field:
| Number | Arbitrary | Negative Values | Positive Values | One | Binary | Currency | Decimal |
| 2.8723 | 1.6733 | 2.8723 | 2.8723 | 0 | 0.4949 | $3,033.4832 | 2.9010 |
Results per field
(c) 2013-2025 Altair Engineering Inc. All Rights Reserved.