Percentile
The selected percentile.
Percentile 
is the value of the P-th percentile of an ascending ordered data set containing N elements with values 
.
There are two steps to compute for Percentile.
- Calculate the rank:
The rank is then split into its integer component k and decimal component d, such that
. - Use the formula below to calculate as:
Sample 1
Consider the ordered list of values 15, 20, 35, 40, 50. What is the 40th percentile of this list?
- Calculate the rank of the 40th percentile as follows.
Thus, n=2.6, which gives us k=2 and d=0.6.
- Calculate the value of the 40th percentile.
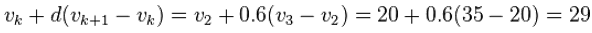
Thus, the value of the 40th percentile of the ordered list 15, 20, 35, 40, 50 is 29.
Sample 2
Consider the ordered list 1,2,3,4. What is the 75th percentile of this list?
- Calculate the rank of the 75th percentile as follows.
N = 75/100(4-1) + 1 = 3.25
Thus, n=3.25, which gives us k=3 and d=0.25.
- Calculate the value of the 75th percentile.
Thus, the value of the 75th percentile of the ordered list 1,2,3,4 is 3.25.
Sample 3
Given the following sample fields:
| Number | Arbitrary | Negative Values | Positive Values | One | Binary | Currency | Decimal |
| 1 | 3 | -1 | 1 | 1 | 0 | $1.00 | 1.01 |
| 2 | 2 | -2 | 2 | 1 | $10.00 | 2.02 | |
| 3 | 1 | -3 | 3 | 0 | $100.00 | 3.03 | |
| 4 | 0 | -4 | 4 | 1 | $1,000.00 | 4.04 | |
| 5 | -1 | -5 | 5 | 0 | $10,000.00 | 5.05 | |
| 6 | -2 | -6 | 6 | 1 | -$1.00 | 6.06 | |
| 7 | -3 | -7 | 7 | 0 | -$10.00 | 7.07 | |
| 8 | 0 | -8 | 8 | -$100.00 | 8.08 | ||
| 9 | 0 | -9 | 9 | -$1,000.00 | 9.09 | ||
| 10 | 0 | -10 | 0 | $0.00 | 0.00 |
Sample fields
The 50th Percentile value for each field in the table:
| Number | Arbitrary | Negative Values | Positive Values | One | Binary | Currency | Decimal |
| 5.50 | 0.00 | -5.50 | 4.50 | 1.00 | 0.00 | 0.50 | 4.55 |
Results per field
(c) 2013-2025 Altair Engineering Inc. All Rights Reserved.