MATHC

Bulk Data Entry This material data defines honeycomb material behavior in Explicit analysis.

The material is used to describe honeycomb and foam with anisotropic behavior. The nonlinear elastoplastic material can be defined separately for all normal and shear behavior for uncompacted configuration, and isotropic material model is considered for a fully compacted model. This material is available for solid elements.

Format


(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
MATHC	`MID`	`E`	`NU`	`RHO`	`SIGY`	`VF`
	`LCA`	`LCB`	`LCC`		`LCAB`	`LCBC`	`LCCA`
	`EAAU`	`EBBU`	`ECCU`	`GABU`	`GBCU`	`GCAU`

Definitions


Field	Contents	SI Unit Example
`MID`	Material identification number. No default (Integer > 0)
`E`	Young's Modulus for the compacted honeycomb material No Default (Real > 0)
`Nu`	Poisson’s ratio for the compacted honeycomb material. No Default (Real > 0)
`RHO`	Mass Density. No Default (Real > 0)
`SIGY`	Yield stress for the fully compacted honeycomb material. No Default (Real > 0)
`VF`	The relative volume at which the honeycomb material is fully compacted. No Default (0 < Real < 1)
`LCA`	Identification number of function for sigaa versus volumetric strain. No Default (Integer > 0)
`LCB`	Identification number of function for sigbb versus volumetric strain. No Default (Integer > 0)
`LCC`	Identification number of function for sigcc versus volumetric strain. No Default (Integer > 0)
`LCAB`	Identification number of function for sigab versus volumetric strain. No Default (Integer > 0)
`LCBC`	Identification number of function for sigbc versus volumetric strain. No Default (Integer > 0)
`LCCA`	Identification number of function for sigca versus volumetric strain. No Default (Integer > 0)
`EAAU`	Initial Young's Modulus Eaa in the uncompacted configuration. No Default (Real > 0)
`EBBU`	Initial Young Modulus Ebb in the uncompacted configuration. No Default (Real > 0)
`ECCU`	Initial Young's Modulus Ecc in the uncompacted configuration. No Default (Real > 0)
`GABU`	Initial shear modulus Gab in the uncompacted configuration. No Default (Real > 0)
`GBCU`	Initial shear modulus Gbc in the uncompacted configuration. No Default (Real > 0)
`GCAU`	Initial shear modulus Gca in uncompacted configuration. No Default (Real > 0)

Comments

General Nonlinear Elastoplastic Behavior

Uncompacted Honeycomb Material V > VF
The Behavior before compaction is orthotropic and the stresses are completely uncoupled. The elastic moduli by direction vary from their initial value to the isotropic fully compacted value E at Vf as:
$E_{a a} = E_{a a u} + β (E - E_{a a u})$
$E_{b b} = E_{b b u} + β (E - E_{b b u})$
$E_{c c} = E_{c c u} + β (E - E_{c c u})$
$G_{a b} = G_{a b u} + β (G - G_{a b u})$
$G_{b c} = G_{b c u} + β (G - G_{b c u})$
$G_{c a} = G_{c a u} + β (G - G_{c a u})$
With $β = \max [Min (\frac{1 - V}{1 - V_{F}}, 0), 1]$ and $G = \frac{E}{2 (1 + ν)}$
V is relative volume and V_F is the relative volume at which the honeycomb is compacted. For the uncompacted configuration the trial stress components are updated as:
$σ_{a a}^{t r i a l} (t_{n + 1}) = σ_{a a}^{t r i a l} (t_{n}) + E_{a a} Δ ϵ_{a a}$
$σ_{b b}^{t r i a l} (t_{n + 1}) = σ_{b b}^{t r i a l} (t_{n}) + E_{b b} Δ ϵ_{b b}$
$σ_{c c}^{t r i a l} (t_{n + 1}) = σ_{c c}^{t r i a l} (t_{n}) + E_{c c} Δ ϵ_{c c}$
$σ_{a b}^{t r i a l} (t_{n + 1}) = σ_{a b}^{t r i a l} (t_{n}) + 2 G_{a b} Δ ϵ_{a b}$
$σ_{b c}^{t r i a l} (t_{n + 1}) = σ_{b c}^{t r i a l} (t_{n}) + 2 G_{b c} Δ ϵ_{b c}$
$σ_{c a}^{t r i a l} (t_{n + 1}) = σ_{c a}^{t r i a l} (t_{n}) + 2 G_{c a} Δ ϵ_{b c}$
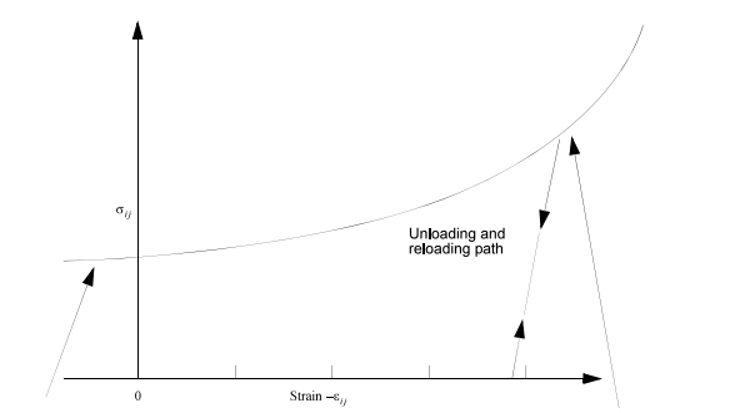
Each stress component must not exceed the permissible values given by the stress versus volumetric strain defined by the curve (LCAA, LCBB, … and so on) for each component.
$|σ_{i j}^{t r i a l} (t_{n + 1})| < σ_{i j} (V)$
Thus,
$σ_{i j} (t_{n + 1}) = σ_{i j} (V) \frac{σ_{i j}^{t r i a l} (t_{n + 1})}{|σ_{i j}^{t r i a l} (t_{n + 1})|}$
The $σ_{i j} (V)$ is defined for each component using LCAA, LCBB, LCCC … (see Figure 1).
Compacted Honeycomb Material V < VF
For the fully compacted honeycomb material, assume the behavior is isotropic and elastic perfectly plastic. Thus, the stress is updated using Hook Material law. So, the deviatoric stresses are given by:
$S_{i j}^{t r i a l} (t_{n + 1}) = S_{i j} (t_{n + 1}) + 2 G Δ ε_{i j}^{d e v}$
Where the deviatoric strain increment is defined by:
$Δ ε_{i j}^{d e v} = ε_{i j} - \frac{1}{3} Δ ε_{k k} δ_{i j}$
The equivalent Von Mises stress of the fully compacted honeycomb material is compared to the SIGY. If the effective stress exceeds the yield stress, the tensor stress is simply scaled back to the yield surface using:
$S_{i j} (t_{n + 1}) = \frac{σ_{y}}{S_{e q}^{t r i a l}} S_{i j}^{t r i a} (t_{n + 1})$
Where $S_{e q}^{t r i a l} = {(\frac{3}{2} S_{i j}^{t r i a} S_{i j}^{t r i a})}^{\frac{1}{2}}$
The pressure is updated using the Bulk modulus as:
$P (t_{n + 1}) = P (t_{n}) - K Δ ε_{k k}$
Where $K = \frac{E}{3 (1 - 2 ν)}$
Thus, the final Cauchy stress is computed as:
$σ_{i j} (t_{n + 1}) = S_{i j} (t_{n + 1}) - P (t_{n + 1}) δ_{i j}$

Figure 1. Stress versus Volumetric Strain