Augmented Lagrange Multiplier (ALM) Method (Nonlinear Analysis)
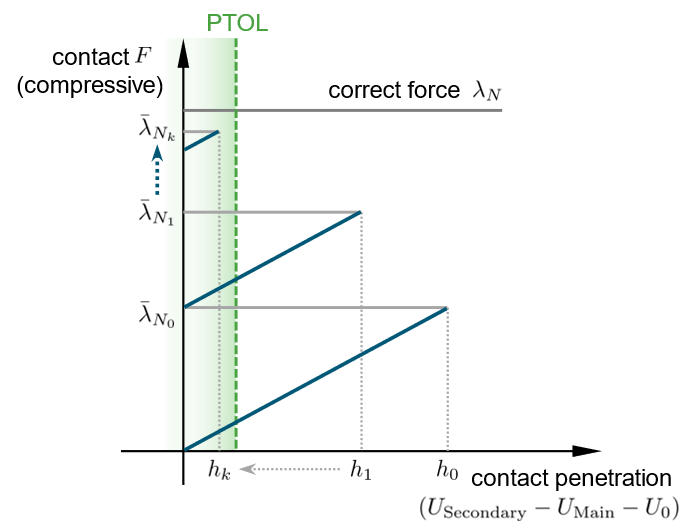
The ALM method does not introduce real Lagrange multipliers as additional unknown variables in the system and can instead be categorized as a variant of the penalty-based method. When the ALM method is activated, the contact pressure data in the last converged results are employed as constant multipliers in the pressure formulation of the succeeding iterations, as shown in the force-penetration curve in Figure 1, where λ ̅_(N k-1) is the normal force obtained from the last converged state. The ALM method uses the contact pressure to determine the open/close status of a contact element.
The ALM method is applicable to Nonlinear Static and Transient Analysis and can be activated by CONTPRM,ALM,YES or the ALM continuation line on the PCONT Bulk Data Entry. Additional augmentations iterations are carried out when a time increment is converged while the penetration tolerance, defined with CONTPRM,ALMPTOL or the PTOL field on the PCONT Bulk Data Entry, is not satisfied.
The schematic augmentation process of the contact force is visualized in Figure 2 where the contact force approaches the correct value after a few augmentations, with the subscript k (k=0, 1, …) denoting the augmentation index. Usually, the default tolerance is recommended such that a balance between accuracy and computational cost is achieved. Pressure augmentation also happens naturally at new time increments without direct augmentation iterations and setting the tolerance too strict may result in excessive number of augmentation iterations.
The ALM method can achieve an accurate result on the contact interface with relatively soft penalty stiffness, though it may result in an increased number of iterations in some cases. The penalty stiffness for the ALM method is controlled by CONTPRM,ALMSFKN or the SFKN field on the PCONT Bulk Data Entry, and is independent of any STIFF options mentioned in the preceding sections. Option SFKN=AUTO determines the value of the normal penalty stiffness for each contact element using the stiffness of surrounding elements along the normal direction of the surface. Generally, the AUTO stiffness for the ALM method is softer than the AUTO stiffness employed in the penalty-based contact. Additional options AUTO, HARD, SOFT or Real<0.0 for SFKN are available as a scaling factor applied on the stiffness value via SFKN=AUTO.