Block Category: Matrix Operation
Inputs: Two or three inputs
c: Column; scalar
r: Row; scalar
bottom input: Matrix or vector
Description: The index block allows you to address a single element within a vector or matrix. The index block can have two or three inputs. When there are two inputs, the top input is always r, which specifies the row, regardless of whether the bottom input is a matrix or vector.
When there are three inputs, the top input r specifies the row, the middle input c specifies the column, and the bottom input is the matrix.
If you address an element outside the bounds of the vector or matrix, the index block displays the following warning message:
Index n too big.
Index n is either 1 or 2, depending on which index exceeds the bounds first.
Referencing matrix elements: Index values map to matrix elements in sequential order, starting with the element in column1-row1, through column1-rowN; then column2-row2 through column2-rowN; and so on. For example, in the following 2 × 3 matrix, an index value of 3 yields 5:
|
1 |
2 |
|
3 |
4 |
|
5 |
6 |
Index value: The following rules apply to the index value:
•Index values that are non-integers are truncated. For example, 0.999 is truncated to 0.
•If the index value targets an unconnected matrix or vector element, the index block outputs a 0.
•If the index value targets an out-of-range matrix or vector element, the index block outputs spurious results. For example, if the index value is 5 for a four-element matrix, the output might look something like this: 1.06983e-306.

Label: Indicates a user-defined block label that appears when View > Block Labels is activated.
1. 3 x 4 matrix
A 3 x 4 matrix is fed into an index block, as shown below.
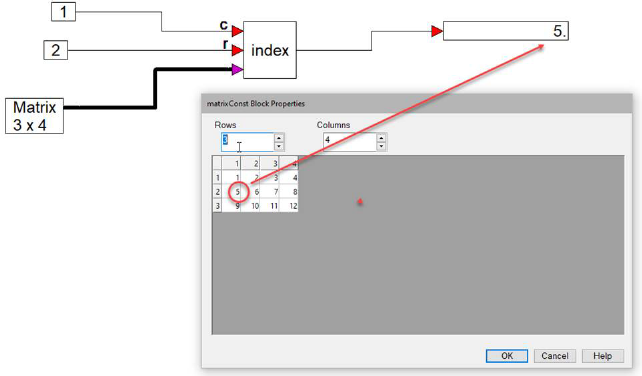
The index block outputs 1, 2, 3, 4, 5, 6, 7,8, 9, 10, 11, or 12 depending on the index input values. In this example, the index value is second row, first column, causing a 5 to be output.