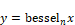
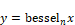
Block Category: Transcendental
Input: Real scalars.
Description: The bessel block generates the Bessel function of order n.
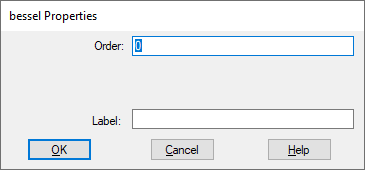
Label: Indicates a user-defined block label that appears when View > Block Labels is activated.
Order: Sets the order of the Bessel function. Specify the order as an integer. You can enter a value in hexadecimal notation or as a C expression. If you specify the order as a C expression, it is converted to an integer. The default is 0.
1. Approximation of sin(a sin φ)
Bessel functions come up frequently in the analysis and solution of nonlinear differential equations. Consider the following approximation:
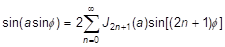
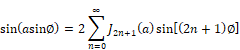
where a and φ are parameters, and Jn is a Bessel function of order n. Such approximations are a part of the standard procedure for obtaining approximate analytical solutions to equations of the type:
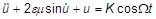
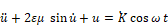
These equations are used in the harmonic analysis of forced oscillations of single degree of freedom systems.
The above approximation is realized as:
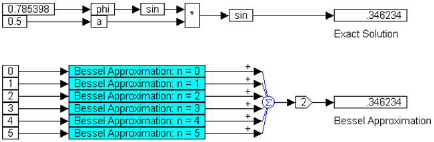
Two const blocks produce π/4 and 0.5 as the values for φ and a, respectively. The sine of phi is multiplied by a and the result is fed through another sin block to compute the exact solution.
Six const blocks, set to 0 through 5, generate different terms of the infinite series approximation. In this case, only the first six terms of the series are retained. Each of these const blocks is connected to a compound block with the following internal structure:
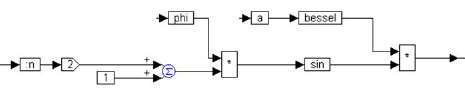
The const block feeds a value to a local variable :n. The output of :n is connected to a gain block set to 2. The output of the gain block and the output of a const block set to 1 are fed into two inputs of a summingJunction block. The output of the summingJunction block and the output of variable phi are connected to a * block to compute the term (2n+1)φ. The variable a is connected to a bessel block whose internal order is set to the correct value (0, 3, 5, 7, 9, or 11, depending on the value of :n).
At the top level, the outputs of the six compound blocks are summed using a six input summingJunction block, and the output of the summingJunction block is connected to a gain block set to 2. The output of the gain block is connected to a display block.
From the results obtained, it is proven that by retaining the first six terms in the approximation, very close agreement can be obtained with the actual value of sin(a sin φ).