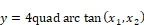
Block Category: Transcendental
Input: Real scalars.
Description: The atan2 block computes the four-quadrant inverse tangent of the input signals. The atan2 block uses the signs of both input signals to determine the sign of the output signal. The output is an angle in radians. For fixed-point implementation, use the fxAtan2 block.
Label: Indicates a user-defined block label that appears when View > Block Labels is activated.
1. Computation of tan-1(∝) = π/2
This equation is realized as:
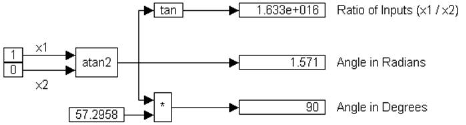
To convert radians to degrees, the angle in radians is multiplied by (180/π) = 57.2958.
Since the atan2 block uses the value of x1, the signs of x1 and x2, and the ratio x1/x2 in computing the inverse tangent, the result depends on all these parameters. In the current case, since the ratio is infinity, atan2 computes the inverse correctly to be π/2 radians, or 90o. Also, in the current case, x1 can be any positive value, since its ratio with 0 will be infinity, regardless of its value.
2. Computation of tan-1(-1): quadrant dependency
Using the same configuration in the above example, tan-1(-1) is realized as:
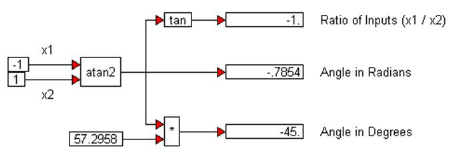
Here, the angle obtained is -0.7854 radians, or -45o, because the atan2 block determines that the angle lies in the fourth quadrant. However, it is immediately apparent that the same ratio of -1 can be obtained by flipping the signs on x1 and x2:
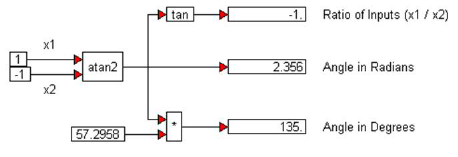
In this case, the atan2 block uses the relative signs of x1 and x2 to determine that the angle lies in the second quadrant, and yields an angle of 180 - 45 = 135o, or 2.356 radians.