UserDefinedComponents

Description

In this section some hints are given to define your own 1-dimensional rotational components which are compatible with the elements of this package. It is convenient to define a new component by inheritance from one of the following base classes, which are defined in sublibrary Interfaces:

Name	Description
PartialCompliant	Compliant connection of two rotational 1-dim. flanges (used for force laws such as a spring or a damper).
PartialCompliantWithRelativeStates	Same as "PartialCompliant", but relative angle and relative speed are defined as preferred states. Use this partial model if the force law needs anyway the relative speed. The advantage is that it is usually better to use relative angles between drive train components as states, especially, if the angle is not limited (e.g., as for drive trains in vehicles).
PartialElementaryTwoFlangesAndSupport2	Partial model for a 1-dim. rotational gear consisting of the flange of an input shaft, the flange of an output shaft and the support.
PartialTorque	Partial model of a torque acting at the flange (accelerates the flange).
PartialTwoFlanges	General connection of two rotational 1-dim. flanges.
PartialAbsoluteSensor	Measure absolute flange variables.
PartialRelativeSensor	Measure relative flange variables.

The difference between these base classes are the auxiliary variables defined in the model and the relations between the flange variables already defined in the base class. For example, in model PartialCompliant there is no support flange, whereas in model PartialElementaryTwoFlangesAndSupport2 there is a support flange.

The equations of a mechanical component are vector equations, i.e., they need to be expressed in a common coordinate system. Therefore, for a component a local axis of rotation has to be defined. All vector quantities, such as cut-torques or angular velocities have to be expressed according to this definition. Examples for such a definition are given in the following figure for an inertia component and a planetary gearbox:

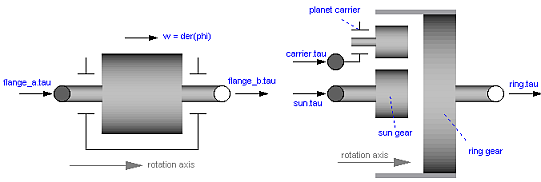
As can be seen, all vectors are directed into the direction of the rotation axis. The angles in the flanges are defined correspondingly. For example, the angle sun.phi in the flange of the sun wheel of the planetary gearbox is positive, if rotated in mathematical positive direction (= counter clock wise) along the axis of rotation.

On first view, one may assume that the selected local coordinate system has an influence on the usage of the component. But this is not the case, as shown in the next figure:

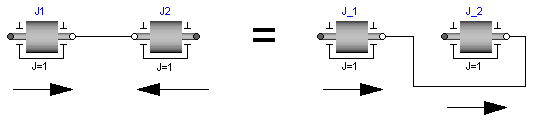
In the figure the local axes of rotation of the components are shown. The connection of two inertias in the left and in the right part of the figure are completely equivalent, i.e., the right part is just a different drawing of the left part. This is due to the fact, that by a connection, the two local coordinate systems are made identical and the (automatically) generated connection equations (= angles are identical, cut-torques sum-up to zero) are also expressed in this common coordinate system. Therefore, even if in the left figure it seems to be that the angular velocity vector of J2 goes from right to left, in reality it goes from left to right as shown in the right part of the figure, where the local coordinate systems are drawn such that they are aligned. Note, that the simple rule stated in section 4 (Sign conventions) also determines that the angular velocity of J2 in the left part of the figure is directed from left to right.

To summarize, the local coordinate system selected for a component is just necessary, in order that the equations of this component are expressed correctly. The selection of the coordinate system is arbitrary and has no influence on the usage of the component. Especially, the actual direction of, e.g., a cut-torque is most easily determined by the rule of section 4. A more strict determination by aligning coordinate systems and then using the vector direction of the local coordinate systems, often requires a re-drawing of the diagram and is therefore less convenient to use.