SupportFriction
Coulomb friction in support
![]()
Library
Modelica/Mechanics/Translational/Components
Description
This element describes Coulomb friction in support, i.e., a frictional force acting between a flange and the housing. The positive sliding friction force "f" has to be defined by table "f_pos" as function of the absolute velocity "v". E.g.
v | f
---+-----
0 | 0
1 | 2
2 | 5
3 | 8
gives the following table:
f_pos = [0, 0; 1, 2; 2, 5; 3, 8];
Currently, only linear interpolation in the table is supported. Outside of the table, extrapolation through the last two table entries is used. It is assumed that the negative sliding friction force has the same characteristic with negative values. Friction is modelled in the following way:
When the absolute velocity "v" is not zero, the friction force is a function of v and of a constant normal force. This dependency is defined via table f_pos and can be determined by measurements, e.g., by driving the gear with constant velocity and measuring the needed driving force (= friction force).
When the absolute velocity becomes zero, the elements connected by the friction element become stuck, i.e., the absolute position remains constant. In this phase the friction force is calculated from a force balance due to the requirement, that the absolute acceleration shall be zero. The elements begin to slide when the friction force exceeds a threshold value, called the maximum static friction force, computed via:
maximum_static_friction = peak * sliding_friction(v=0) (peak >= 1)
This procedure is implemented in a "clean" way by state events and leads to continuous/discrete systems of equations if friction elements are dynamically coupled which have to be solved by appropriate numerical methods. The method is described in (see also a short sketch in UsersGuide.ModelingOfFriction):
- Otter M., Elmqvist H., and Mattsson S.E. (1999):
- Hybrid Modeling in Modelica based on the Synchronous Data Flow Principle. CACSD'99, Aug. 22.-26, Hawaii.
More precise friction models take into account the elasticity of the material when the two elements are "stuck", as well as other effects, like hysteresis. This has the advantage that the friction element can be completely described by a differential equation without events. The drawback is that the system becomes stiff (about 10-20 times slower simulation) and that more material constants have to be supplied which requires more sophisticated identification. For more details, see the following references, especially (Armstrong and Canudas de Wit 1996):
- Armstrong B. (1991):
- Control of Machines with Friction. Kluwer Academic
Press, Boston MA.
- Armstrong B., and Canudas de Wit C. (1996):
- Friction Modeling and Compensation.
The Control Handbook, edited by W.S.Levine, CRC Press,
pp. 1369-1382.
- Canudas de Wit C., Olsson H., Åström K.J., and Lischinsky P. (1995):
- A new model for control of systems with friction.
IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425.
Parameters
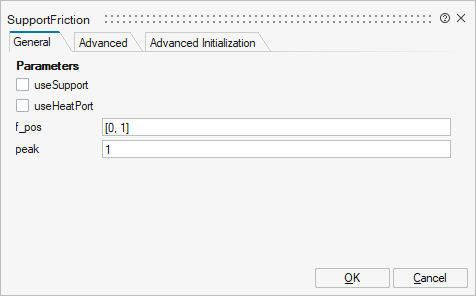
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo_useSupport | useSupport | = true, if support flange enabled, otherwise implicitly grounded | Number | 0 |
mo_useHeatPort | useHeatPort | =true, if heatPort is enabled | Number | 0 |
mo_f_pos | f_pos | [v, f] Positive sliding friction characteristic (v>=0) | Matrix of size Mx2 | |
mo_peak | peak | Peak for maximum friction force at w==0 (f0_max = peak*f_pos[1,2]) | Scalar | |
mo_Unknown | Unknown | Value of mode is not known | Scalar | |
mo_Free | Free | Element is not active | Scalar | |
mo_Forward | Forward | v_relfric > 0 (forward sliding) | Scalar | |
mo_Stuck | Stuck | v_relfric = 0 (forward sliding, locked or backward sliding) | Scalar | |
mo_Backward | Backward | v_relfric < 0 (backward sliding) | Scalar | |
mo_unitAcceleration | unitAcceleration | Scalar | ||
mo_unitForce | unitForce | Scalar |
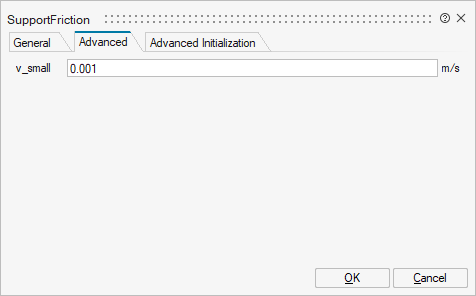
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo_v_small | v_small | Relative velocity near to zero (see model info text) | Scalar |
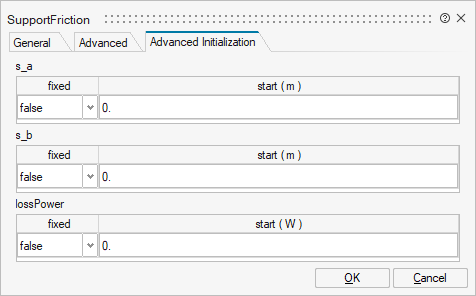
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo_s_a | s_a | s_a | Structure | |
mo_s_a/fixed | fixed | Cell of scalars | true | |
mo_s_a/start | start | Cell of scalars | ||
mo_s_b | s_b | s_b | Structure | |
mo_s_b/fixed | fixed | Cell of scalars | true | |
mo_s_b/start | start | Cell of scalars | ||
mo_lossPower | lossPower | lossPower | Structure | |
mo_lossPower/fixed | fixed | Cell of scalars | true | |
mo_lossPower/start | start | Cell of scalars | ||
mo_v_relfric | v_relfric | v_relfric | Structure | |
mo_v_relfric/fixed | fixed | Cell of scalars | true | |
mo_v_relfric/start | start | Cell of scalars | ||
mo_a_relfric | a_relfric | a_relfric | Structure | |
mo_a_relfric/fixed | fixed | Cell of scalars | true | |
mo_a_relfric/start | start | Cell of scalars | ||
mo_f0 | f0 | f0 | Structure | |
mo_f0/fixed | fixed | Cell of scalars | true | |
mo_f0/start | start | Cell of scalars | ||
mo_f0_max | f0_max | f0_max | Structure | |
mo_f0_max/fixed | fixed | Cell of scalars | true | |
mo_f0_max/start | start | Cell of scalars | ||
mo_free | free | free | Structure | |
mo_free/fixed | fixed | Cell of scalars | true | |
mo_free/start | start | Cell of scalars | ||
mo_sa | sa | sa | Structure | |
mo_sa/fixed | fixed | Cell of scalars | true | |
mo_sa/start | start | Cell of scalars | ||
mo_startForward | startForward | startForward | Structure | |
mo_startForward/fixed | fixed | Cell of scalars | true | |
mo_startForward/start | start | Cell of scalars | ||
mo_startBackward | startBackward | startBackward | Structure | |
mo_startBackward/fixed | fixed | Cell of scalars | true | |
mo_startBackward/start | start | Cell of scalars | ||
mo_locked | locked | locked | Structure | |
mo_locked/fixed | fixed | Cell of scalars | true | |
mo_locked/start | start | Cell of scalars | ||
mo_mode | mode | mode | Structure | |
mo_mode/fixed | fixed | Cell of scalars | true | |
mo_mode/start | start | Cell of scalars | ||
mo_s | s | s | Structure | |
mo_s/fixed | fixed | Cell of scalars | true | |
mo_s/start | start | Cell of scalars | ||
mo_f | f | f | Structure | |
mo_f/fixed | fixed | Cell of scalars | true | |
mo_f/start | start | Cell of scalars | ||
mo_v | v | v | Structure | |
mo_v/fixed | fixed | Cell of scalars | true | |
mo_v/start | start | Cell of scalars | ||
mo_a | a | a | Structure | |
mo_a/fixed | fixed | Cell of scalars | true | |
mo_a/start | start | Cell of scalars |
Ports
| Name | Type | Description | IO Type | Number |
|---|---|---|---|---|
flange_a | implicit | Flange of left shaft | input | 1 |
flange_b | implicit | Flange of right shaft | output | 1 |
Port 3 | implicit | Support/housing of component | input | mo_useSupport |
Port 4 | implicit | Optional port to which dissipated losses are transported in form of heat | input | mo_useHeatPort |