CustomLiquid
Basic graphical layout of input/output block
![]()
Library
HydraulicsByFluidon/Media
Description
Model of a custom hydraulic liquid. The model provides the other components (e.g. pipes) with user-defined temperature- and pressure-dependent fluid properties. In order for the fluid properties to reach the other components, the liquid model must be connected to the hydraulic circuit.
The underlying model is based on the following assumptions:
- In the vicinity of the Reference pressure p0 and Reference temperature T0, the density changes linearly with pressure p and temperature T. Hence, the Isothermal bulk modulus and the Thermal expansion coefficient are constants.
- The change of kinematic viscosity with respect to temperature follows the law proposed by Ubbelohde and Walther (DIN 51563).
- The kinematic viscosity is not affected by the pressure level.
- The specific thermal capacity at constant pressure is a constant.
The density is calculated by the following equation:
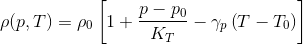
The isentropic bulk modulus is given by:
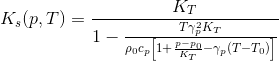
In order to use the component, the following parameters have to be provided by the user:
- Reference pressure p0 and temperature T0 to calculate the density
- Density rho0 at Reference pressure and temperature
- Isothermal bulk modulus Kt and Thermal expansion coefficient Gammap
- Specific heat capacity cp at constant pressure
- Kinematic viscosities nu1 and nu2 at ambient pressure for two different temperatures T1 and T2
If the effects of undissolved air are to be considered during the simulation, the user can provide the fraction of undissolved air at ambient pressure through the parameter Proportion of undissolved air. The stiffness of the gas bubbles is calculated based on the parameter Polytropic exponent which can assume values between 1.0 (isothermal change of state, slow compression/expansion) and 1.4 (isentropic change of state, fast compression/expansion).
Parameters
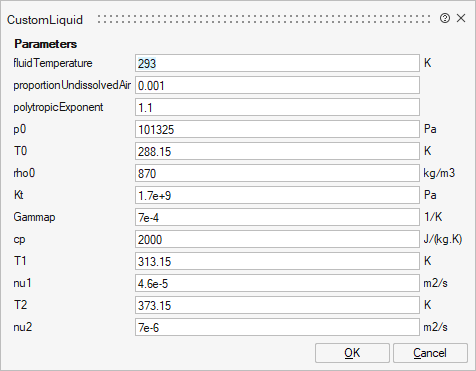
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
mo_fluidTemperature | fluidTemperature | Scalar | ||
mo_proportionUndissolvedAir | proportionUndissolvedAir | Proportion of undissolved air | Scalar | |
mo_polytropicExponent | polytropicExponent | Polytropic exponent | Scalar | |
mo_p0 | p0 | Reference pressure for density calculation | Scalar | |
mo_T0 | T0 | Reference temperature for density calculation | Scalar | |
mo_rho0 | rho0 | Density of fluid at reference temperature and pressure | Scalar | |
mo_Kt | Kt | Isothermal bulk modulus | Scalar | |
mo_Gammap | Gammap | Thermal expansion coefficient | Scalar | |
mo_cp | cp | Specific heat capacity at constant pressure | Scalar | |
mo_T1 | T1 | First reference temperature for viscosity calculation | Scalar | |
mo_nu1 | nu1 | Kinematic viscosity at T1 and ambient pressure | Scalar | |
mo_T2 | T2 | Second reference temperature for viscosity calculation | Scalar | |
mo_nu2 | nu2 | Kinematic viscosity at T2 and ambient pressure | Scalar |
Ports
| Name | Type | Description | IO Type | Number |
|---|---|---|---|---|
fluidPort | implicit | Hydraulic port | input | 1 |