Bobyqa
This block finds the least value of a function of many variables by applying a trust region method that forms quadratic models by interpolation. Some freedom is usually present in the interpolation conditions, which are taken up by minimizing the Frobenius norm of the change to the second derivative of the model, beginning with the zero matrix. The values of the variables are constrained by upper and lower bounds.
![]()
Library
Activate/Optimization
Description
This block implements the Bobyqa optimization program in reverse communication mode. When activated, the block expects to receive on its input ports respectively the value of the optimization vector p and the associated cost. The block then produces on its first output either a new guess value of p for which it expects a cost evaluation at the next iteration, or the optimal solution. In the latter case, the block sets its output, iter (second output), to zero, and the last output, cost_opt, to the cost of the optimal solution. The output iter indicates whether or not an additional iteration is needed. If iter=0, then the optimal value of the cost associated with the optimal p is also produced on the last block output.
For more details, see the section on Optimization in the Extended Definitions for Advanced Users.For further explanation of the BOBYQA algorithm, see: www.damtp.cam.ac.uk/user/na/NA_papers/NA2009_06.pdfParameters
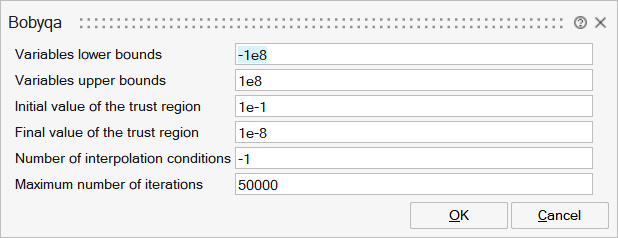
| Name | Label | Description | Data Type | Valid Values |
|---|---|---|---|---|
xL | Variables lower bounds | Matrix of size Mx1 | ||
xU | Variables upper bounds | Matrix of size Mx1 | ||
RhoBeg | Initial value of the trust region | Matrix of size 1x1 | ||
RhoEnd | Final value of the trust region | Matrix of size 1x1 | ||
Npt | Number of interpolation conditions | Scalar | ||
MaxIter | Maximum number of iterations | Scalar |
Ports
| Name | Type | Description | IO Type | Number |
|---|---|---|---|---|
p0 | explicit | input | 1 | |
cost | explicit | input | 2 | |
p | explicit | output | 1 | |
iter | explicit | output | 2 | |
cost_opt | explicit | output | 3 | |
Port 6 | activation | input | 1 |