|
Stdev
The Standard Deviation of the selection.
The Standard Deviation is a measure of how spread-out numbers are in a set. The Deviation just means how far from the normal.
Stdev is used when the group of numbers being evaluated is only a partial sampling of the whole population.
The formula:
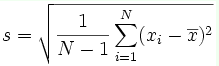
Wher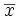e 
is the
mean computed by getting the sum of all the items and dividing them
by the number of items minus one.
Sample 1
Given a set of numbers like 12, 6, 12.
Steps:
1. Compute the mean of the sample.
Mean = (Sum of items/n), where n is the number of items
12+6+12/3=10
2. Square the difference between each point and the mean
(12-10)^2 =4
(6-10)^2 =16
(12-10)^2 =4
3. Calculate the average of the results in step 2 above
4+16+4/3-1=24/2
4. Compute the square root of the result in step 4.
√12 or 3.4641
Sample 2:
Given the following sample fields:
|
Number |
Arbitrary |
Negative Values |
Positive Values |
One |
Binary |
Currency |
Decimal |
|
1 |
3 |
-1 |
1 |
1 |
0 |
$1.00 |
1.01 |
|
2 |
2 |
-2 |
2 |
|
1 |
$10.00 |
2.02 |
|
3 |
1 |
-3 |
3 |
|
0 |
$100.00 |
3.03 |
|
4 |
0 |
-4 |
4 |
|
1 |
$1,000.00 |
4.04 |
|
5 |
-1 |
-5 |
5 |
|
0 |
$10,000.00 |
5.05 |
|
6 |
-2 |
-6 |
6 |
|
1 |
-$1.00 |
6.06 |
|
7 |
-3 |
-7 |
7 |
|
0 |
-$10.00 |
7.07 |
|
8 |
0 |
-8 |
8 |
|
|
-$100.00 |
8.08 |
|
9 |
0 |
-9 |
9 |
|
|
-$1,000.00 |
9.09 |
|
10 |
0 |
-10 |
0 |
|
|
$0.00 |
0.00 |
Sample fields.
The Stdev for each field:
|
Number |
Arbitrary |
Negative Values |
Positive Values |
One |
Binary |
Currency |
Decimal |
|
3.0277 |
1.7638 |
3.0277 |
3.0277 |
0 |
.5345 |
$3,197.5720 |
3.0579 |
The results per field.